题目内容
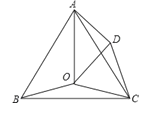
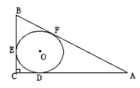
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)求证:OD∥BC;
(2)若AC=2BC,求证:DA与⊙O相切.
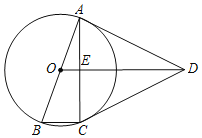
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用SSS可证明△OAD≌△OCD,可得∠ADO=∠CDO,根据等腰三角形“三线合一”的性质可得DE⊥AC,由AB是直径可得∠ACB=90°,即可证明OD//BC;
(2)设BC=a,则AC=2a,利用勾股定理可得AD=AB=![]() ,根据中位线的性质可用a表示出OE、AE的长,即可表示出OD的长,根据勾股定理逆定理可得∠OAD=90°,即可证明DA与⊙O相切.
,根据中位线的性质可用a表示出OE、AE的长,即可表示出OD的长,根据勾股定理逆定理可得∠OAD=90°,即可证明DA与⊙O相切.
(1)连接OC,
在△OAD和△OCD中,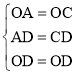 ,
,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
∵AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∴OD∥BC;
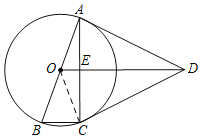
(2)设BC=a,
∵AC=2BC,
∴AC=2a,
∴AD=AB=![]() =
=![]() =
=![]() a,
a,
∵OE∥BC,且AO=BO,
∴OE为△ABC的中位线,
∴OE=![]() BC=
BC=![]() a,AE=CE=
a,AE=CE=![]() AC=a,
AC=a,
在△AED中,DE=![]() =
=![]() =2a,
=2a,
∴OD=OE+DE=![]() ,
,
在△AOD中,AO2+AD2=(![]() )2+(
)2+(![]() a)2=
a)2=![]() a2,OD2=(
a2,OD2=(![]() )2=
)2=![]() a2,
a2,
∴AO2+AD2=OD2,
∴∠OAD=90°,
∵AB是直径,
∴DA与⊙O相切.

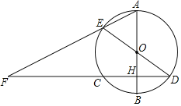
【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

【题目】如图为某商场的一个可以自由转动的转盘,规定:顾客购物满100元即可获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“钦料”的次数m | 71 | 110 | 155 | 379 | 603 | 752 |
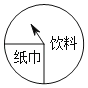
根据以上信息,解决下列问题:
(1)请估计转动该转盘一次,获得饮料的概率约是 (精确到0.01);
(2)现有若干个除颜色外相同的白球和黑球,根据(1)结论,在保证获得饮料与纸巾概率不变的情况下,请你设计一个可行的摸球抽奖规则,详细说明步骤;
(3)若小郑和小刘都购买超过100元的商品,均获得一次转动转盘的机会,请根据(2)中设计的规则,利用列表法或画树状图法求两人都获得“饮料”的概率.