题目内容
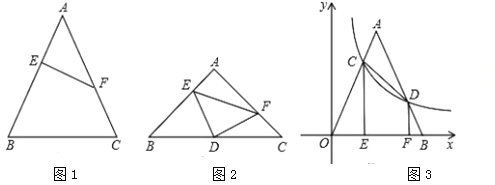
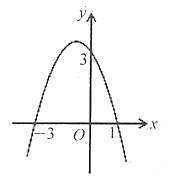
【题目】如图所示是二次函数![]() 的图象,下列结论:
的图象,下列结论:
①二次三项式![]() 的最大值为
的最大值为![]() ;
;
![]() 使
使![]() 成立的
成立的![]() 的取值范围是
的取值范围是![]() ;
;
![]() 一元二次方程
一元二次方程![]() ,当
,当![]() 时,方程总有两个不相等的实数根;
时,方程总有两个不相等的实数根;
![]() 该抛物线的对称轴是直线
该抛物线的对称轴是直线![]() ;
;
![]()
其中正确的结论有______________ (把所有正确结论的序号都填在横线上)
【答案】①③④
【解析】
根据图象求出二次函数的解析式,根据二次函数的性质结合图象可以判断各个小题中的结论是否正确.
由函数图象可知:抛物线过(-3,0),(1,0),(0,3),
∴设抛物线解析式为![]() ,把(0,3)代入得:3=
,把(0,3)代入得:3=![]() ,解得:a=-1,
,解得:a=-1,
∴抛物线为![]() ,即
,即![]() ,
,
∴二次三项式ax2+bx+c的最大值为4,故①正确,
由![]() =3,解得:x=0或x=-2,由图像可知:使y≤3成立的x的取值范围是x≤﹣2或x≥0,故②错误.
=3,解得:x=0或x=-2,由图像可知:使y≤3成立的x的取值范围是x≤﹣2或x≥0,故②错误.
∵二次三项式ax2+bx+c的最大值为4,
∴当k<4时,直线y=k与抛物线![]() 有两个交点,
有两个交点,
∴当k<4时,方程一元二次方程![]() 总有两个不相等的实数根,故③正确,
总有两个不相等的实数根,故③正确,
该抛物线的对称轴是直线x=﹣1,故④正确,
当x=﹣2时,y=4a﹣2b+c>0,故⑤错误.
故答案为:①③④.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目