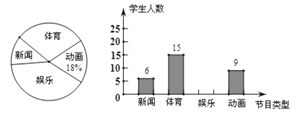
题目内容
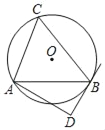
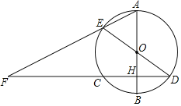
【题目】如图,AB,DE为⊙O的直径,过点D作弦DC⊥AB于点H,连接AE并延长交DC的延长线于点F.
(1)求证:![]()
(2)若sinD=![]() ,求tanF.
,求tanF.
【答案】(1)见解析;(2)![]()
![]()
【解析】
(1)连接OC,先证∠DOH=∠COH,再证∠COH=∠AOE,由圆心角、弧、弦的关系可推出结论;
(2)连接EC,用特殊值法,设OH=3,OD=5,求出CD的长,利用勾股定理求出CE的长,再证△EFC∽△AFH,可求出FC的长,即可求出tanF.
(1)连接OC
∵OC=OD,AB⊥CD
∴∠DOH=∠COH,
∵∠DOH=∠AOE,
∴∠COH=∠AOE,
∴![]() ;
;
(2)连接EC,
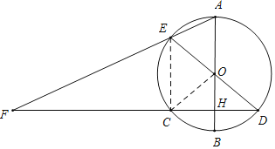
∵AB⊥CD,
∴∠AHD=90°,
∵sin D=![]() ,
,
不妨设OH=3,OD=5,
∴DH=![]() ,
,
∵AB⊥CD,
∴CD=2DH=8,
∵DE为⊙O的直径,
∴∠ECD=90°,
∴CE=![]() ,
,
设FC=![]() ,则FH=
,则FH=![]() ,
,
∵∠AHD=∠ECD=90°,
∴EC∥AH
∴△EFC∽△AFH,
∴![]() ,
,
即![]() ,
,
解得:![]() ,
,
∴![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目