题目内容
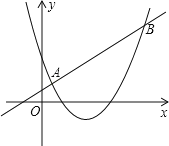
【题目】已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示，它们的两个交点的横坐标是1和4，那么能够使得y1＜y2的自变量x的取值范围是 ．
【答案】x＞4或x＜1
【解析】
试题分析：求能够使得y1＜y2的自变量x的取值范围，实质上就是根据图象找出函数y1=kx+m的值小于y2=ax2+bx+c的值时x的取值范围，由两个函数图象的交点横坐标及图象的位置，可求范围．
解：依题意得，能够使得y1＜y2的自变量x的取值范围，
实质上就是根据图象找出函数y1=kx+m的值小于y2=ax2+bx+c的值时x的取值范围，
由两个函数图象的交点横坐标及图象的位置可以知道此时x的取值范围x＞4或x＜1．
故填空答案：x＞4或x＜1．
练习册系列答案
相关题目
