题目内容
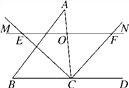
【题目】如图,点C在AB上,![]() 、
、![]() 均是等边三角形,
均是等边三角形,![]() 、
、![]() 分别与
分别与![]() 交于点
交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() 为等边三角形;④
为等边三角形;④![]() ∥
∥![]() ;⑤DC=DN正确的有( )个
;⑤DC=DN正确的有( )个
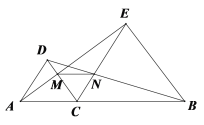
A.2个B.3个C.4个D.5
【答案】C
【解析】
首先根据等边三角形的性质,运用SAS证明△ACE≌△DCB,即可得出AE=DB;再由ASA判定△AMC≌△DNC,得出CM=CN;由∠MCN=60°得出△CMN为等边三角形;再由内错角相等两直线平行得出MN∥BC;最后由∠DCN=∠CNM=60°,得出DC≠DN,即可判定.
∵![]() 、
、![]() 均是等边三角形,
均是等边三角形,
∴∠DCA=∠ECB=60°,AC=DC,EC=BC
∴∠DCE=60°
∴∠DCA+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB
∴△ACE≌△DCB(SAS)
∴AE=DB,故①正确;
∵△ACE≌△DCB,
∴∠MAC=∠NDC,
∵∠ACD=∠BCE=60°,
∴∠MCA=∠DCN=60°,
在△AMC和△DNC中
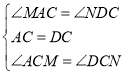
∴△AMC≌△DNC(ASA),
∴CM=CN,故②正确;
∴△CMN为等边三角形,故③正确;
∴∠NMC=∠NCB=60°,
∴MN∥BC.故④正确;
∵∠DCN=∠CNM=60°
∴DC≠DN,故⑤错误;
故选:C.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目