题目内容
【题目】如图,已知直线![]() :
:![]() 与x轴,y轴的交点分别为A,B,直线
与x轴,y轴的交点分别为A,B,直线![]() :
: ![]() 与y轴交于点C,直线
与y轴交于点C,直线![]() 与直线
与直线![]() 的交点为E,且点E的横坐标为2.
的交点为E,且点E的横坐标为2.
(1)求实数b的值;
(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线![]() 与直线
与直线![]() 于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.

【答案】(1)3;(2)a=5或-1.
【解析】
(1)利用一次函数图象上点的坐标特征,由点E在直线![]() 上可得到点E的坐标,由点E在直线
上可得到点E的坐标,由点E在直线![]() 上,进而得出实数b的值;
上,进而得出实数b的值;
(2)依据题意可得MN=|1+![]() a(3
a(3![]() a)|=|a2|,BO=3.当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,即可得到|a-2|=3,进而得出a的值.
a)|=|a2|,BO=3.当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,即可得到|a-2|=3,进而得出a的值.
解:(1)∵点E在直线l1上,且点E的横坐标为2,
∴点E的坐标为(2,2),
∵点E在直线l上,
∴2=![]() ×2+b,
×2+b,
解得:b=3;
(2)如图,当x=a时,yM=3![]() a,yN=1+
a,yN=1+![]() a,
a,
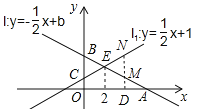
∴MN=|1+![]() a(3
a(3![]() a)|=|a2|,
a)|=|a2|,
当x=0时,yB=3,
∴BO=3.
∵BO∥MN,
∴当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,
此时|a-2|=3,
解得:a=5或a=-1.
∴当以点B、O、M、N为顶点的四边形为平行四边形,a的值为5或-1.
故答案为:(1)3;(2)a=5或-1.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目