Question

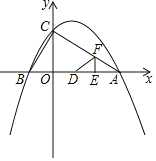
【题目】如图，在Rt△ABC中，CD，CE分别是斜边AB上的高，中线，BC＝a，AC＝b．

（1）若a＝3，b＝4，求DE的长；

（2）直接写出：CD＝　 　（用含a，b的代数式表示）；

（3）若b＝3，tan∠DCE=，求a的值．

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）求出BE，BD即可解决问题．

（2）利用勾股定理，面积法求高CD即可．

（3）根据CD＝3DE，构建方程即可解决问题．

解：（1）在Rt△ABC中，∵∠ACB＝90°，a＝3，b＝4，

∴．

∵CD，CE是斜边AB上的高，中线，

∴∠BDC＝90°，．

∴在Rt△BCD中，

（2）在Rt△ABC中，∵∠ACB＝90°，BC＝a，AC＝b，

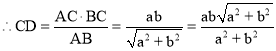故答案为：．

（3）在Rt△BCD中，，

∴，

又，

∴CD＝3DE，即．

∵b＝3，

∴2a＝9﹣a2，即a2+2a﹣9＝0．

由求根公式得（负值舍去），

即所求a的值是．