题目内容
【题目】如图,点![]() 是
是![]() 内的一点,过点
内的一点,过点![]() 分别作直线平行于
分别作直线平行于![]() 的各边,所形成的三个小三角形
的各边,所形成的三个小三角形![]() ,
,![]() ,
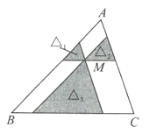
,![]() (图中阴影部分)的面积分别是4、9、49,求
(图中阴影部分)的面积分别是4、9、49,求![]() 的面积.
的面积.
【答案】144
【解析】
根据相似三角形的面积比是相似比的平方,先求出相似比.再根据平行四边形的性质及相似三角形的性质得到BC:DM=6:1,即![]() ,从而得到△ABC面积.
,从而得到△ABC面积.
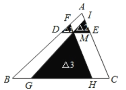
解:过M作BC的平行线交AB、AC于D、E,过M作AC的平行线交AB、BC于F、H,过M作AB的平行线交AC、BC于I、G,
∵![]() ,
,![]() ,
,![]() 的面积比为4:9:49,
的面积比为4:9:49,
∴他们对应边边长的比为2:3:7,
又∵四边形BDMG与四边形CEMH为平行四边形,
∴DM=BG,EM=CH,
设DM为2x,则ME=3x,GH=7x,
∴BC=BG+GH+CH=DM+GH+ME=2x+3x+7x=12x,
∴BC:DM=12x:2x=6:1,
由面积比等于相似比的平方故可得出:![]() ,
,
∴![]() .
.

练习册系列答案
相关题目