Question

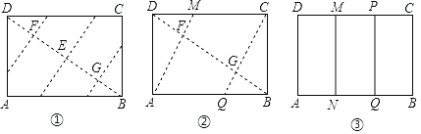
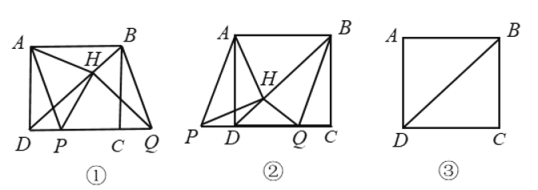
【题目】如图，已知矩形纸片ABCD，怎样折叠，能使边AB被三等分？

以下是小红的研究过程．

思考过程	要使边AB被三等分，若从边DC上考虑，就是要折出DM＝DC， 也就是要折出DM＝AB， 当DB、AM相交于F时，即要折出对角线上的DF＝DB．那么…
折叠方法和示意图	①折出DB；对折纸片，使D、B重合，得到的折痕与DB相交于点E；继续折叠纸片，使D、B与E重合，得到的折痕与DB分别相交于点F、G； ②折出AF、CG，分别交边CD、AB于M、Q； ③过M折纸片，使D落在MC上，得到折痕MN，则边AB被N、Q三等分．

（1）整理小红的研究过程，说明AN＝NQ＝QB；

（2）用一种与小红不同的方法折叠，使边AB被三等分．（需简述折叠方法并画出示意图）

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）由折叠的性质可得DF＝DB，DM＝AN，通过证明DFM∽BAF，可得DM＝AB，可得AN＝AB，同理可求QB＝AB，可得结论；

（2）所求图形，如图所示，由折叠的性质可得AF＝BF＝DE＝EC＝CD，AN＝DM＝NQ，通过证明AGF∽CGD，可得，由平行线分线段成比例可得AN＝MC＝DM，即可证AN＝NQ＝QB．

解：（1）由折叠的性质可得，DF＝DB，四边形ADMN是矩形，

∴DM＝AN，

∵CD∥AB，

∴DFM∽BAF，

∴＝，

∴DM＝AB，

∴AN＝AB，

同理可求QB＝AB，

∴AN＝NQ＝QB；

（2）如图，

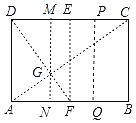
①将矩形ABCD对折，使AD与BC重合，折痕为EF；

②连接AC，DF，交点为G，

③过点G折叠矩形ABCD，使点D落在CE上，对应点为E，

使点A落在BF上，对应点为Q，折痕为MN；

∴点N，点Q为AB的三等分点．

理由如下：由折叠的性质可得：AF＝BF＝DE＝EC＝CD，AN＝DM＝NQ，

∵AB∥CD，

∴AGF∽CGD，

∴，

∵AB∥CD，

∴，

∴AN＝MC＝DM，

∴AN＝DM＝CD＝AB，

∴NQ＝AB，

∴AN＝NQ＝QB．