题目内容
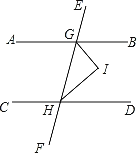
【题目】如图，已知AB∥CD，直线EF分别交直线AB、CD于点G、H，GI、HI分别平分∠BGH、∠GHD．
（1）求证GI⊥HI．
（2）请用文字概括（1）所证明的命题： ．
【答案】（1）见解析；（2）两直线平行，同旁内角的角平分线互相垂直
【解析】
利用角平分线、平行线的性质及三角形的内角和定理，先求出∠I的度数，再说明两直线的关系．
证明：（1）∵AB
CD，
∴∠BGH+∠GHD＝180°．
∵∠HGI＝
∠HGB，∠GHI＝∠GHD，
∴∠HGI+∠GHI＝∠HGB+∠GHD
＝（∠HGB+∠GHD）
＝90°．
∵∠HGI+∠KHI+∠I＝180°，
∴∠I＝90°．
∴GI
HI．
（2）文字可概况为：两直线平行，同旁内角的角平分线互相垂直．
故答案为：两直线平行，同旁内角的角平分线互相垂直．
阅读快车系列答案
【题目】某水果店计划购进甲、乙两种高档水果共400千克，每千克的售价、成本与购进数量（千克）之间关系如表：
每千克售价（元） | 每千克成本（元） | |
甲 | ﹣0.1x+100 | 50 |
乙 | ﹣0.2x+120（0＜x≤200） | 60 |
|
（1）若甲、乙两种水果全部售完，求水果店获得总利润y（元）与购进乙种水果x（千克）之间的函数关系式（其他成本不计）；
（2）若购进两种水果都不少于100千克，当两种水果全部售完，水果能获得的最大利润．
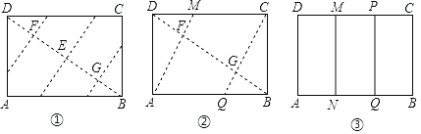
【题目】如图，已知矩形纸片ABCD，怎样折叠，能使边AB被三等分？
以下是小红的研究过程．
思考过程 | 要使边AB被三等分，若从边DC上考虑，就是要折出DM＝ 也就是要折出DM＝ 当DB、AM相交于F时，即要折出对角线上的DF＝ |
折叠方法和示意图 | ①折出DB；对折纸片，使D、B重合，得到的折痕与DB相交于点E；继续折叠纸片，使D、B与E重合，得到的折痕与DB分别相交于点F、G； ②折出AF、CG，分别交边CD、AB于M、Q； ③过M折纸片，使D落在MC上，得到折痕MN，则边AB被N、Q三等分．
|
（1）整理小红的研究过程，说明AN＝NQ＝QB；
（2）用一种与小红不同的方法折叠，使边AB被三等分．（需简述折叠方法并画出示意图）
