题目内容
【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
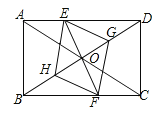
【答案】(1)见解析;(2)四边形EGFH是菱形,理由见解析
【解析】
(1)由平行四边形的性质得出AD∥BC,AD=BC,OB=OD,由平行线的性质得出∠FBH=∠EDG,∠OHF=∠OGE,得出∠BHF=∠DGE,求出BF=DE,由AAS即可得出结论;
(2)先证明四边形EGFH是平行四边形,再由等腰三角形的性质得出EF⊥GH,即可得出四边形EGFH是菱形.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,
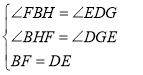 ,
,
∴BFH≌△DEG(AAS);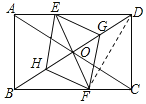
(2)解:四边形EGFH是菱形;理由如下:
连接DF,设EF交BD于O.如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵DE=BF,∠EOD=∠BOF,∠EDO=∠FBO,
∴△EDO≌△FBO,
∴OB=OD,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.

 作业辅导系列答案
作业辅导系列答案【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项,每4年评选一次,在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家,美籍华人丘成桐1982年获得费尔兹奖.为了让学生了解费尔兹奖得主的年龄情况,我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1(数据分成5组,各组是28≤x<31,31≤x<34,34≤x<37,37≤x<40,x≥40):
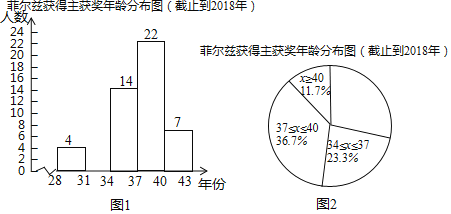
b.如图2,在a的基础上,画出扇形统计图;
c.截止到2018年费尔兹奖得主获奖时的年龄在34≤x<37这一组的数据是:
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d.截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下:
年份 | 平均数 | 中位数 | 众数 |
截止到2018 | 35.58 | m | 37,38 |
根据以上信息,回答下列问题:
(1)依据题意,补全频数直方图;
(2)31≤x<34这组的圆心角度数是度,并补全扇形统计图;
(3)统计表中中位数m的值是;
(4)根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征.