题目内容
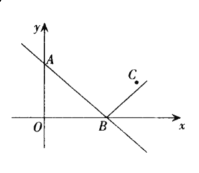
【题目】如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线![]() 恰好经过边AB的四等分点E(BE<AE),则k的值为____________.
恰好经过边AB的四等分点E(BE<AE),则k的值为____________.

【答案】-![]()
【解析】
由AD∥BC,可得出S△BCD=S△BCA、S△ACD=S△ABD,根据△ACD与△BCD的面积分别为10和20结合同底三角形面积的性质,即可得出AO:OC=DO:OB=1:2,进而可得出S△AOB=![]() ,再根据反比例函数系数k的几何意义以及相似三角形的性质得出|k|=
,再根据反比例函数系数k的几何意义以及相似三角形的性质得出|k|=![]() ,解之即可得出结论.
,解之即可得出结论.
∵AD∥BC,
∴S△BCD=S△BCA,S△ACD=S△ABD.
∵△ACD与△BCD的面积分别为10和20,
∴△ABD和△BCD面积比为1:2,
∴根据同底得:AO:OC=DO:OB=1:2,
∴S△AOB=![]() .
.
∵双曲线![]() 恰好经过边AB的四等分点E(BE<AE),
恰好经过边AB的四等分点E(BE<AE),
∴![]() S△AOB+|k|+
S△AOB+|k|+![]() S△AOB=S△AOB,
S△AOB=S△AOB,
∴|k|=![]() S△AOB=
S△AOB=![]() ,
,
∵双曲线经过第二象限,k<0,
∴k=-![]() .
.
故答案为-![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目