题目内容
【题目】在平面直角坐标系中，过格点A、B、C作一圆弧．
（1）弧AC的长为_____（结果保留π）；
（2）点B与图中格点的连线中，能够与该圆弧相切的连线所对应的格点的坐标为_____．
【答案】(1)
（2）（5，1）或（1，3）或（7，0）
【解析】
（1）根据垂径定理的推论：弦的垂直平分线必过圆心，可以作弦AB和BC的垂直平分线，交点即为圆心，然后根据弧长的公式即刻得到结论；
（2）由弦AB与弦BC的垂直平分线的交点为圆心，找出圆心O′的位置，确定出圆心坐标，过点B与圆相切时，根据切线的判定方法得到∠O′BF为直角时，BF与圆相切，根据网格找出满足条件的F坐标即可．
(1)根据过格点A，B，C作一圆弧，
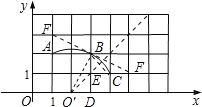
由图形可得：三点组成的圆的圆心为：O′(2,0)，
∴半径
连接
则
∴弧AC的长
故答案为：
(2)∵由图形可得：三点组成的圆的圆心为：O′(2,0)，
∴只有
时，BF与圆相切，
此时△BO′D≌△FBE，EF=BD=2，
∴F点的坐标为：(5,1)或(1,3)或(7,0)，
则点B与下列格点的连线中,能够与该圆弧相切的是(5,1)或(1,3)或(7,0)，共3个.
故答案为：(5,1)或(1,3)或(7,0).
练习册系列答案
阅读快车系列答案
相关题目
