Question

【题目】下列说法中错误的有（ ）

（1）两边及其中一边上的中线对应相等的两个三角形全等

（2）两边及第三边上的中线对应相等的两个三角形全等

（3）两边及其中一边上的高对应相等的两个三角形全等

（4）两边及第三边上的高对应相等的两个三角形全等

（5）两角及夹边上的高对应相等的两个三角形全等

A.0个B.1个C.2个D.3个

Answer 1

【答案】C

【解析】

根据题意画出图形，利用全等三角形的判定定理逐一判断.

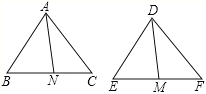
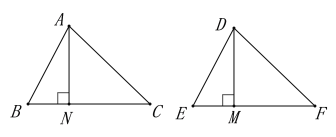
解：（1）如图，已知AB=DE，BC=EF，AN、DM是△ABC和△DEF的中线，且AN=DM

∵AN、DM是△ABC和△DEF的中线，BC=EF，

∴BN=EM，

∵AB=DE，BN=EM ，AN=DM，

∴△ABN≌△DEM（SSS），

∴∠B=∠E，

∵AB=DE，∠B=∠E， BC=EF，

∴△ABC≌△DEF（SAS）.

故（1）选项正确；

（2）根据题中条件不能证明两三角形全等，故（2）选项错误；

（3）如图，已知AB=DE，BC=EF，AN、DM是△ABC和△DEF的高，且AN=DM

∵AN、DM是△ABC和△DEF的高，

∴∠ANB=∠DME=90°，

∵AB=DE，AN=DM，

∴Rt△ABN≌Rt△DEM（HL），

∴∠B=∠E，

∵AB=DE，∠B=∠E， BC=EF，

∴△ABC≌△DEF（SAS）.

故（3）选项正确；

（4）因为两边及其中一边的对角相等的两三角形不一定全等，根据题中条件不能证明两三角形全等，故（4）选项错误；

（5）如图，已知∠B=∠E, ∠C=∠F，AN、DM是△ABC和△DEF的高，且AN=DM

∵AN、DM是△ABC和△DEF的高，

∴∠ANB=∠DME=90°，

∵∠ANB=∠DME，∠B=∠E，AN=DM，

∴△ABN≌△DEM（AAS），

∴AB=DE，

∵AB=DE，∠B=∠E，∠C=∠F，

∴△ABC≌△DEF（AAS）.

故（5）选项正确；

故说法错误的有2个.

故选：C