题目内容
6、如图所示，四边形ABCD的AD∥BC，DF=CF，连接AF交BC延长线于E点，图中哪两个三角形可以通过怎样的旋转而相互得到的？分析：∵AD∥BC，DF=CF，∴△ADF≌△ECF，∴FA=FE．已知FD=FC，可确定点F为旋转中心，旋转角180°，△ECF与△ADF可以通过互相旋转得到．
解答：解：图中△ADF绕着F旋转180°可以到△ECF的位置，也可以说△ECF绕着F旋转180°可以到△ADF的位置．
点评：本题考查运用旋转的性质，寻找旋转图形的方法，关键是确定旋转中心和对应点，对应线段．
练习册系列答案
相关题目
21、如图所示，四边形ABCD是平行四边形，E，F分别在AD，CB的延长线上，且DE=BF，连接FE分别交AB，CD于点H，G．
12、如图所示，四边形ABCD为⊙O的内接四边形，E为AB延长线的上一点，∠CBE=40°，则∠AOC等于（ ）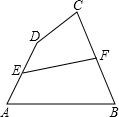
如图所示，四边形ABCD中，E、F分别为AD、BC的中点．
