题目内容
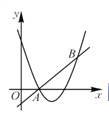
【题目】如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集(直接写出答案);
(3)若M(a,y1),N(a+1,y2)两点都在抛物线y=x2+bx+c上,试比较y1与y2的大小.
【答案】(1) m=-1.抛物线的解析式为y=x2-3x+2.
(2)x>3或x<1.
(3)当2a-2<0,即a<1时,y1>y2;
当2a-2=0,即a=1时,y1=y2;
当2a-2>0,即a>1时,y1<y2.
【解析】试题分析:(1)分别把点A(1,0),B(3,2)代入直线y=x+m和抛物线y=x2+bx+c,利用待定系数法解得y=x﹣1,y=x2﹣3x+2;
(2)根据题意列出不等式,直接解二元一次不等式即可,或者根据图象可知,x2﹣3x+2>x﹣1的图象上x的范围是x<1或x>3;
(3)直接根据函数图象即可得出结论.
试题解析:解:(1)∵把点A(1,0),B(3,2)分别代入直线y=x+m和抛物线y=x2+bx+c得:
0=1+m, ![]() ,∴m=﹣1,b=﹣3,c=2,∴y=x﹣1,y=x2﹣3x+2;
,∴m=﹣1,b=﹣3,c=2,∴y=x﹣1,y=x2﹣3x+2;
(2)由函数图象可知,当x<1或x>3时,不等式x2+bx+c>x+m的解集;
(3)将M(a,y1),N(a+1,y2)两点代入y=x2﹣3x+2,得:
y1=a2﹣3a+2,y2=(a+1)2﹣3(a+1)+2=a2﹣a.
则y1﹣y2=a2﹣3a+2﹣(a2﹣a)=2﹣2a.
①当2﹣2a>0,即a<1时,y1>y2;
②当2﹣2a=0,即a=1时,y1=y2;
③当2﹣2a<0,即a>1时,y1<y2;
所以当a<1时,y1>y2;当a=1时,y1=y2;当a>1时,y1<y2;


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





