题目内容
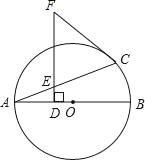
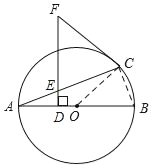
【题目】如图,AB是⊙O的直径,F是⊙O外一点,过点F作FD⊥AB于点D,交弦AC于点E,且FC=FE.
(1)求证:FC是⊙O的切线;
(2)若⊙O的半径为5,cos∠FCE=![]() ,求弦AC的长.
,求弦AC的长.
【答案】(1)证明见解析(2)2![]()
【解析】
(1)连接OC,因为FC=FE,所以∠FCE=∠FEC,又因为FD⊥AB,所以∠OAC+∠AED=90°,所以∠OCA+∠FCE=90°,从而可得∠OCF=90°.
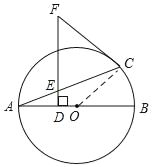
(2)连接BC,由(1)可知:∠AED=∠FCE,因为AB是⊙O的直径,所以∠ACB=90°,由于∠CAB+∠AED=90°,∠CAB+∠B=90°,所以∠B=∠AED=∠FCE,最后利用锐角三角函数的定义即可求出答案.
(1)连接OC,
∵FC=FE,
∴∠FCE=∠FEC,
∵∠FEC=∠AED,
∴∠AED=∠FCE,
∵OA=OC,
∴∠OAC=∠ACO,
∵FD⊥AB,
∴∠OAC+∠AED=90°,
∴∠OCA+∠FCE=90°,
∴∠OCF=90°,
∵OC是⊙O的半径,
∴FC是⊙O的切线;
(2)连接BC,
由(1)可知:∠AED=∠FCE,
∵AB是⊙O的直径,
∴∠ACB=90°
∵∠CAB+∠AED=90°,∠CAB+∠B=90°
∴∠B=∠AED=∠FCE,
∴cos∠FCE=cos∠B=![]() ,
,
∴BC=4,
∴由勾股定理可知:AC=2![]()

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目