题目内容
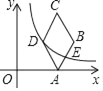
【题目】发现问题:如图1,直线a∥b,点B、C在直线b上,点D为AC的中点,过点D的直线与a,b分别相交于M、N两点,与BA的延长线交于点P,若△ABC的面积为1,则四边形AMNB的面积为 ;
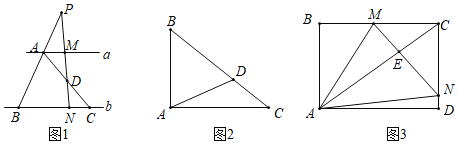
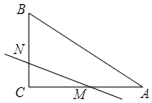
探究问题:如图2,Rt△ABC中,∠DAC=![]() ∠BAC,DA=2,求△ABC面积的最小值;
∠BAC,DA=2,求△ABC面积的最小值;
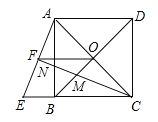
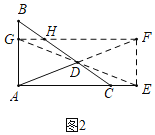
拓展应用:如图3,矩形花园ABCD的长AD为400米,宽CD为300米,供水点E在小路AC上,且AE=2CE,现想沿BC上一点M和CD上一点N修一条小路MN,使得MN经过E,并在四边形AMCN围城的区域内种植花卉,剩余区域铺设草坪根据项目的要求种植花卉的区域要尽量小.请根据相关数据求出四边形AMCN面积的最小值,及面积取最小时点M、N的位置.(小路的宽忽略不计)
【答案】发现问题: S四边形AMNB =1;探究问题:当BC与GE重合时,△ABC的面积最小,最小值为2![]() ;拓展应用:四边形AMCN的面积的最小值=80000平方米,此时CM=CF=GH=
;拓展应用:四边形AMCN的面积的最小值=80000平方米,此时CM=CF=GH=![]() 米,CN=CH=200米
米,CN=CH=200米
【解析】
发现问题:证明△ADM≌△CDN(ASA),即可解决问题;
探究问题:如图2中,延长AD到F,使得DF=DA,作FG⊥AB于G,FE⊥AC交AC的延长线于E,利用矩形是中心对称图形,过对称中心的直线平分矩形的面积解决问题即可;
拓展应用:如图3中,取AE的中点G,作GH⊥CD于H,GF⊥BC于F,连接FH.首先证明S四边形AMCN=3S△CMN,当△CMN的面积最小时,四边形AMCN的面积最小,利用探究问题中的方法解决问题即可.
发现问题:如图1中,
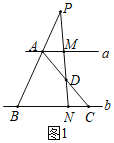
∵a∥b,
∴∠MAD=∠NCD,
∵AD=DC,∠ADM=∠CDN,
∴△ADM≌△CDN(ASA),
∴S△ADM=S△CDN,
∴S四边形AMNB=S△ABC=1,
故答案为1.
探究问题:如图2中,延长AD到F,使得DF=DA,作FG⊥AB于G,FE⊥AC交AC的延长线于E,
∵∠FEA=∠FGA=∠GAE=90°,
∴四边形AEFG是矩形,
∵∠DAC=![]() ∠BAC=30°,AD=DF=2,
∠BAC=30°,AD=DF=2,
∴AF=4,EF=![]() AF=2,AE=
AF=2,AE=![]() EF=2
EF=2![]() ,
,
∴S矩形AEFG=4![]() ,
,
∵矩形AEFG是中心对称图形,D是对称中心,
∴过点D的任意直线平分矩形AEFG的面积,
∴S四边形ACGH=![]() S矩形ABCD=2
S矩形ABCD=2![]() ,
,
∵S△ABC≥S四边形ACHG,
∴S△ABC≥2![]() ,
,
∴当BC与GE重合时,△ABC的面积最小,最小值为2![]() .
.
拓展应用:如图3中,取AE的中点G,作GH⊥CD于H,GF⊥BC于F,连接FH.
易知四边形GHCF是矩形,
∵AE=2EC,AG=EG,
∴EC=EG,
∴点E在FH上,
∵AC=3EC,
∴S△ACM=3S△ECM,S△ACN=3S△ECN,
∴S四边形AMCN=3S△CMN,
∴当△CMN的面积最小时,四边形AMCN的面积最小,
∵矩形CFGH是中心对称图形,
由探究问题可知:当MN与FH重合时,△MCN的面积最小,
AC=![]() =500(米),
=500(米),
∴CG=![]() ×500=
×500=![]() (米),
(米),
∵GH∥AD,
∴![]() ,
,
∴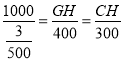 ,
,
∴GH=![]() (米),CH=200(米),
(米),CH=200(米),
∴△MCN的面积的最小值=![]() (平方米),
(平方米),
∴四边形AMCN的面积的最小值=80000(平方米),此时CM=CF=GH=![]() (米),CN=CH=200(米)
(米),CN=CH=200(米)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案