题目内容
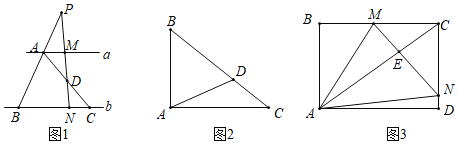
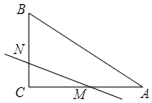
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,点M是AC边的中点,点N是BC边上的任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为_____.
【答案】![]() 或
或![]()
【解析】
根据题意分三种情况讨论,分别作图取BC、AB的中点H、G,连接MH、HG、MG,①当点C′落在MH上时,设NC=NC′=x,则MC=MC′=4,MH=5,HC′=1,HN=3﹣x,根据Rt△HNC′中,HN2=HC′2+NC′2,列式求解;②当点C′落在GH上时,设NC=NC′=x,Rt△GMC′中,MG=CH=3,MC=MC′=4,求出GC′=![]() ,再证明△HNC′∽△GC′M,根据
,再证明△HNC′∽△GC′M,根据![]() ,即可求出x,③,当点C′落在直线GM上时,易证四边形MCNC′是正方形,可得CN=CM=2,由C'M>GM,故点C′在中位线GM的延长线上,不符合题意.
,即可求出x,③,当点C′落在直线GM上时,易证四边形MCNC′是正方形,可得CN=CM=2,由C'M>GM,故点C′在中位线GM的延长线上,不符合题意.
解:取BC、AB的中点H、G,连接MH、HG、MG.
如图1中,当点C′落在MH上时,设NC=NC′=x,
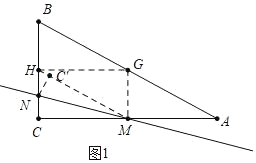
由题意可知:MC=MC′=4,MH=5,HC′=1,HN=3﹣x,
在Rt△HNC′中,∵HN2=HC′2+NC′2,
∴(3﹣x)2=x2+12,
解得x=![]() .
.
如图2中,当点C′落在GH上时,设NC=NC′=x,
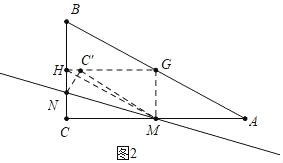
在Rt△GMC′中,MG=CH=3,MC=MC′=4,
∴GC′=![]() ,
,
∵∠NHC'=∠C'GM=90°,∠NC'M=90°,
∴∠HNC'+∠HC'N=∠GC'M+∠HC'N=90°,
∴∠HNC'=∠CGC'M,
∴△HNC′∽△GC′M,
∴![]() ,
,
∴![]() ,
,
∴x=![]() .
.
如图3中,当点C′落在直线GM上时,易证四边形MCNC′是正方形,可得CN=CM=2.
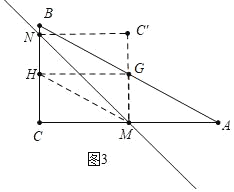
∴C'M>GM,
此时点C′在中位线GM的延长线上,不符合题意.
综上所述,满足条件的线段CN的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.