题目内容
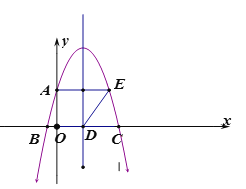
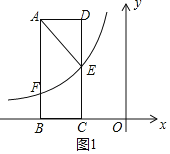
【题目】如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.
(1)若点B坐标为(﹣6,0),求直线AE的表达式;
(2)反比例函数y=![]() (x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(3)在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.

【答案】(1)y=﹣![]() x;(2)y=﹣
x;(2)y=﹣![]() ;(3)
;(3)![]() <n≤2.
<n≤2.
【解析】
(1)由矩形的性质结合点B的坐标,可得出点A,E的坐标,再利用待定系数法即可求出直线AE的表达式;(2)由DC的长结合反比例函数图象上点的坐标特征,可得出点E的坐标为(![]() ,4),在Rt△ADE中,利用勾股定理可求出AE的长,结合AF﹣AE=2可得出AF的长,由BC=3可得出点F的坐标为(
,4),在Rt△ADE中,利用勾股定理可求出AE的长,结合AF﹣AE=2可得出AF的长,由BC=3可得出点F的坐标为(![]() ﹣3,1),再利用反比例函数图象上点的坐标特征,可得出关于m的一元一次方程,解之即可得出m的值,进而可得出反比例函数的表达式;(3)由(2)可得出点M,N的坐标,结合平移的性质可得出平移后点M,N的坐标,设设点P的坐标为(﹣
﹣3,1),再利用反比例函数图象上点的坐标特征,可得出关于m的一元一次方程,解之即可得出m的值,进而可得出反比例函数的表达式;(3)由(2)可得出点M,N的坐标,结合平移的性质可得出平移后点M,N的坐标,设设点P的坐标为(﹣![]() +n,y),由点P在MN上且MP<NP,可得出y的取值范围,利用反比例函数图象上点的坐标特征,可得出关于n的一元一次不等式组,解之即可得出n的取值范围.
+n,y),由点P在MN上且MP<NP,可得出y的取值范围,利用反比例函数图象上点的坐标特征,可得出关于n的一元一次不等式组,解之即可得出n的取值范围.
(1)由题意,可知:点A的坐标为(﹣6,8),点E的坐标为(﹣3,4).
设直线AE的表达式为y=kx+b(k≠0),
将A(﹣6,8),E(﹣3,4)代入y=kx+b,得: ![]() ,
,
解得: ,
,
∴当点B的坐标为(﹣6,0)时,直线AE的表达式为y=﹣![]() x.
x.
(2)∵反比例函数y=![]() 的图象经过点E,E是DC的中点,DC=8,
的图象经过点E,E是DC的中点,DC=8,
∴点E的坐标为(![]() ,4).
,4).
在Rt△ADE中,AD=3,DE=4,∠ADE=90°,
∴AE=![]() =5.
=5.
∵AF﹣AE=2,
∴AF=7,
∴BF=AB﹣AF=1,
∴点F的坐标为(![]() ﹣3,1).
﹣3,1).
∵点F在反比例函数y=![]() 的图象上,
的图象上,
∴![]() ﹣3=m,
﹣3=m,
解得:m=﹣4,
∴反比例函数的表达式为y=﹣![]() .
.
(3)由(2)可知:点B的坐标为(﹣4,0),点C的坐标为(﹣1,0),
∴点M的坐标为(﹣![]() ,8),点N的坐标为(﹣
,8),点N的坐标为(﹣![]() ,0),
,0),
∴平移后的点M的坐标为(﹣![]() +n,8),平移后点N的坐标为(﹣
+n,8),平移后点N的坐标为(﹣![]() +n,0).
+n,0).

设点P的坐标为(﹣![]() +n,y),∵点P在MN上,且MP<NP,
+n,y),∵点P在MN上,且MP<NP,
∴4<y≤8.
∵点P在反比例函数y=﹣![]() 的图象上,
的图象上,
∴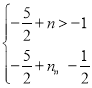 ,
,
解得:![]() <n≤2.
<n≤2.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案