题目内容
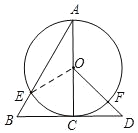
【题目】如图，AC是⊙O的直径，∠A＝30°，BD是⊙O的切线，C为切点，AB与⊙O相交于点E，OC＝CD，BC＝2，OD与⊙O相交于点F，则弧EF的长为（ ）
A.
B.
C.
D.
【答案】D
【解析】
连结OE，由条件可得AC⊥BD，因为OC=CD，所以∠COD=45°，因为BC=2，∠A=30°，所以∠EOC=60°，AC=2
，即∠EOF=105°，OC=，再代入弧长计算公式即可得出弧EF的长．
解：如图，连结OE，
∵AC是⊙O的直径，BD是⊙O的切线，C为切点，
∴AC⊥BD，
∵OC＝CD，
∴∠COD＝45°，
∵BC＝2，∠A＝30°，
∴∠EOC＝2∠A＝60°，AC＝2，
∴∠EOF＝∠EOC+∠COD＝60°+45°＝105°，OC＝，
∴弧EF的长为：
．
故选：D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
