题目内容
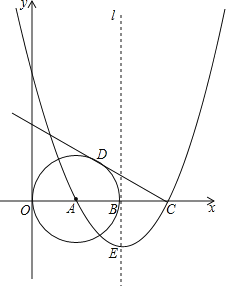
【题目】如图,已知点A(2,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A,抛物线与x轴的另一个交点为点C,抛物线的顶点为点E,如果CO=2BE,求此抛物线的解析式;
(2)过点C作⊙A的切线CD,D为切点,求此切线长;
(3)点F是切线CD上的一个动点,当△BFC与△CAD相似时,求出BF的长.
【答案】(1)y=![]() (x-2)(x-6);(2)CD=2
(x-2)(x-6);(2)CD=2![]() ;(3)BF的长为
;(3)BF的长为![]() 或
或![]() .
.
【解析】
(1)由题意可知抛物线的对称轴为x=4,然后设出抛物线的两点式,然后将点E的坐标代入求解即可;
(2)由于AD是⊙A的切线,连接AD,那么根据切线的性质知AD⊥CD,在Rt△ACD中,可利用勾股定理求得切线CD的长度;
(3)若△BFC与△CAD相似,则有两种情况需要考虑:①△FBC∽△ADC,②△BFC∽△CAD,根据不同的相似三角形所得不同的比例线段即可求得CF的长.
(1)∵A(2,0),⊙A与y轴切于原点,
∴⊙A的半径为2.
∴点B的坐标为为(4,0).
∵点A、C关于x=4对称,
∴C(6,0).
又CO=2BE,
∴E(4,-3)
设抛物线的解析式为y=a(x-2)(x-6),(a≠0);
∵抛物线经过点E(4,-3)
∴-3=a(4-2)(4-6),
解得:a=![]() .
.
∴抛物线的解析式为y=![]() (x-2)(x-6);
(x-2)(x-6);
(2)如图1所示:连接AD,
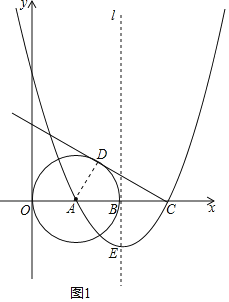
∵AD是⊙A的切线,
∴∠ADC=90°,AD=2,
由(1)知,C(6,0).
∵A(2,0),
∴AC=4,
在Rt△ACD中,CD2=AC2-AD2=42-22=12,
∴CD=2![]() .
.
(3)如图2所示:当FB⊥AD时,连结AD.
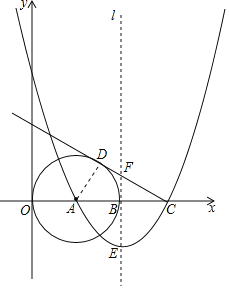
∵∠FBC=∠ADC=90°,∠FCB=∠ACD,
∴△FBC∽△ADC,
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
解得:CF=![]() .
.
如图3所示:当BF⊥CD时,连结AD、过点B作BF⊥CD,垂足为F.
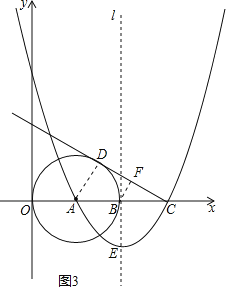
∵AD⊥CD,
∴BF∥AD,
∴△BFC∽△ADC,
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴CF=![]() .
.
综上所述,BF的长为![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知二次函数y=ax2-4x+c,函数值y与自变量x之间的部分对应值如表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 15 | m | n | 0 | k | … |
(1)求这个二次函数的关系式.
(2)直接写出m、n、k之间的大小关系.(用“>”连接)
(3)若点P在这个二次函数的图象上,且点P到x轴的距离为1,求点P的坐标.