Question

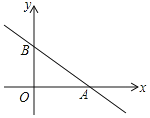
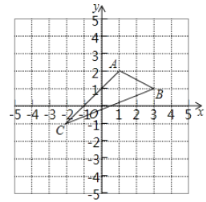
【题目】如图，A，B是直线y=x+4与坐标轴的交点，直线y=-2x+b过点B，与x轴交于点C．

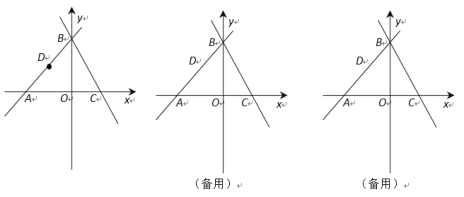
（1）求A，B，C三点的坐标；

（2）点D是折线A—B—C上一动点．

①当点D是AB的中点时，在x轴上找一点E，使ED+EB的和最小，用直尺和圆规画出点E的位置（保留作图痕迹，不要求写作法和证明），并求E点的坐标．

②是否存在点D，使△ACD为直角三角形，若存在，直接写出D点的坐标；若不存在，请说明理由

Answer 1

【答案】（1）A(-4，0) ；B(0，4)；C(2，0)；（2）①点E的位置见解析，E（，0）；②D点的坐标为（-1，3）或（，）

【解析】

（1）先利用一次函数图象上点的坐标特点求得点A、B的坐标；然后把B点坐标代入y=2x＋b求出b的值，确定此函数解析式，然后再求C点坐标；
（2）①根据轴对称—最短路径问题画出点E的位置，由待定系数法确定直线DB1的解析式为y=3x4，易得点E的坐标；
②分两种情况：当点D在AB上时，当点D在BC上时．当点D在AB上时，由等腰直角三角形的性质求得D点的坐标为（1，3）；当点D在BC上时，设AD交y轴于点F，证△AOF与△BOC全等，得OF=2，点F的坐标为（0，2），求得直线AD的解析式为，与y=2x＋4组成方程组，求得交点D的坐标为（，）．

（1）在y=x +4中，

令x =0，得y=4，

令y =0，得x=-4，

∴A(-4，0) ，B(0，4)

把B(0，4)代入y=-2x+b，得b =4，

∴直线BC为：y=-2x+4

在y=-2x +4中，

令y =0，得x=2，

∴C点的坐标为(2，0)；

（2）①如图

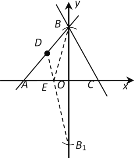
∵点D是AB的中点

∴D（-2，2）

点B关于x轴的对称点B1的坐标为（0，-4），

设直线DB1的解析式为，

把D（-2，2），B1（0，-4）代入，得，

解得k=-3，b=-4，

∴该直线为：y=-3x-4，

令y=0，得x=，

∴E点的坐标为（，0）．

②存在，D点的坐标为（-1，3）或（，）．

当点D在AB上时，

∵OA=OB=4，

∴∠BAC=45°，

∴△ACD是以∠ADC为直角的等腰直角三角形，

∴点D的横坐标为，

当x=-1时，y=x+4=3，

∴D点的坐标为（-1，3）；

当点D在BC上时，如图，设AD交y轴于点F．

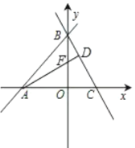
∵∠FAO＋∠AFO＝∠CBO＋∠BFD，∠AFO＝∠BFD，

∴∠FAO=∠CBO，

又∵AO=BO，∠AOF=∠BOC，

∴△AOF≌△BOC（ASA）

∴OF=OC=2，

∴点F的坐标为（0，2），

设直线AD的解析式为，

将A（-4，0）与F（0，2）代入得，

解得，

∴，

联立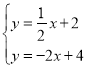，解得：，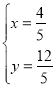

∴D的坐标为（，）．

综上所述：D点的坐标为（-1，3）或（，）