题目内容
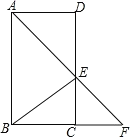
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)因为四边形![]() 是平行四边形,所以根据条件证明
是平行四边形,所以根据条件证明![]() 即可;(2)过点B作
即可;(2)过点B作![]() 于点H,在Rt△BCE中,由勾股定理求出
于点H,在Rt△BCE中,由勾股定理求出![]() ,在Rt△AHB中,求出
,在Rt△AHB中,求出![]() ,然后根据定义可求sin∠AEB的值.
,然后根据定义可求sin∠AEB的值.
试题解析:(1)证明:![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() //BC.
//BC.
![]() ∠DAF=∠F.
∠DAF=∠F.
![]() ∠F=45°,
∠F=45°,
![]() ∠DAE=45°. 1分
∠DAE=45°. 1分
![]() AF是∠BAD的平分线,
AF是∠BAD的平分线,
![]() .
.
![]() .
.
又![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 四边形ABCD是矩形. 2分
四边形ABCD是矩形. 2分
(2)解:过点B作![]() 于点H,如图.
于点H,如图.
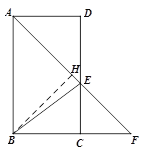
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,
![]() AB=CD,AD=BC,∠DCB=∠D=90°.
AB=CD,AD=BC,∠DCB=∠D=90°.
![]() AB=14,DE=8,
AB=14,DE=8,
![]() CE=6.
CE=6.
在Rt△ADE中,∠DAE=45°,
![]() ∠DEA=∠DAE=45°.
∠DEA=∠DAE=45°.
![]() AD=
AD=![]() =8.
=8.
![]() BC=8.
BC=8.
在Rt△BCE中,由勾股定理得
![]() . 3分
. 3分
在Rt△AHB中,∠HAB=45°,
![]()
![]() . 4分
. 4分
![]() 在Rt△BHE中,∠BHE=90°,
在Rt△BHE中,∠BHE=90°,
![]() sin∠AEB=
sin∠AEB=![]() . 5分
. 5分

练习册系列答案
相关题目