Question

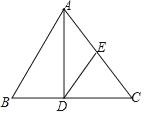
【题目】已知：如图，在△ABC中，AD是边BC上的高，E为边AC的中点，BC=21，AD=8，sinB=．

求：（1）线段DC的长；

（2）tan∠EDC的值．

Answer 1

【答案】（1）15；（2）

【解析】

第（1）问中要求CD的长，已知条件中给出了BC的长，这时只要求出BD的长即可；

利用三角函数的定义和AD的长可以得到AB的长，再在Rt△ABD中利用勾股定理得到BD的长，继而求出CD的长；

第（2）问是求一个锐角的正切值，需要放在直角三角形中求解，因此，要求tan∠CDE的值，就需将∠CDE进行转化；

利用直角三角形斜边上的中线可以得到DE=EC，进而得到∠EDC=∠ECD，从而将问题转化为求∠EDC的正切值.

解：（1）∵AD是BC边上的高，△ABD和△ACD是直角三角形，

在Rt△ABD中，∵sinB=，AD=8，

∴=，

∴AB=10，

∴BD==6，

又∵BC=21，

∴CD=BC﹣BD=15；

（2）在Rt△ACD中，

∵E为斜边AC的中点，

∴ED=EC=AC，

∴∠C=∠EDC，

∴tan∠EDC=tanC==．