Question

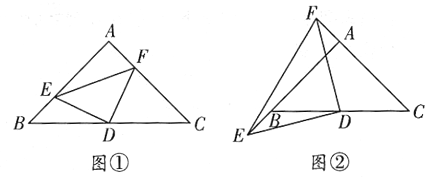
【题目】已知：如图①，在等腰直角中，斜边．

（1）请你在图①的边上求作一点，使得；

（2）如图②，在（1）问的条件下，将边沿方向平移，使得点、、对应点分别为、、，连接，．若平移的距离为1，求的大小及此时四边形的面积；

（3）将边沿方向平移个单位至，是否存在这样的，使得在直线上有一点，满足，且此时四边形的面积最大？若存在，求出四边形面积的最大值及平移距离的值；若不存在，请说明理由．

Answer 1

【答案】（1）详见解析；（2），；（3）存在，当时，四边形面积最大值为

【解析】

（1）利用等腰三角形“三线合一”的性质，取AC中点为点P即可．

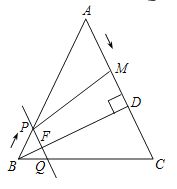
（2）延长AP、CD相交于点M，取AB的中点F，连接PF．证明△APE≌△MPD，得到AP=MP，从而可得PF是△ABM的中位线．进而得到PF是AB的垂直平分线，这样可以得出∠APB=2∠M=2∠EAP．由AE=PE可得∠M=∠MPD=∠EPA=∠EAP，所以可得∠PDB=2∠M，由AC∥ED可得∠PDB=∠ACB=45°，所以∠APB=45°．

（3）如图，以AB为边长，在直线AB的右侧作等边三角形ABO，在以O为圆心、OA长为半径作⊙O．过点O作OM⊥AC，交⊙O于点M，点M在AC的右上方．过点M作AC的平行线DE，AE∥BC，BC的延长线交DE于点D．则此时满足∠AMB=30°，此时四边形ABDE的面积最大．

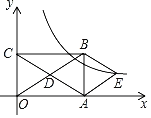
解：(1)利用等腰三角形的“三线合一”性质，取AC的中点P，连接BP即可，如下图所示：

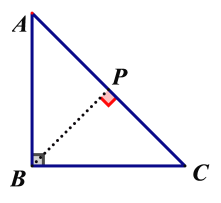
(2)如下图所示：

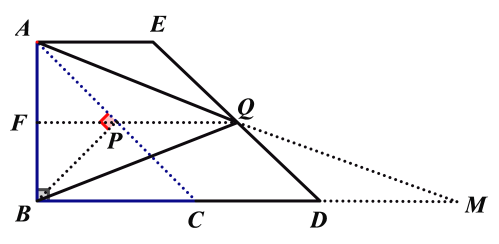
延长AQ、CD相交于点M，取AB的中点F，连接PF．

由平移的性质可得，DE=AC=2，AE=CD=1，AC∥DE，AE∥CD

设∠EAQ=x

∵点Q是DE的中点∴QE=QD=DE=1

∴QE=AE

∴∠AQE=∠EAQ=x，∴∠MQD=∠AQE=x

∵AE∥CD ∴∠M=∠EAQ=x

在△AQE和△MQD中

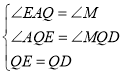，∴△AQE≌△MQD(AAS)

∴AQ=MQ

∵点F是AB的中点

∴QF是△ABM的中位线

∵由题知，∠ABC=90°

∴∠AFQ=90°

∴PF⊥AB，点F是AB的中点

∴BQ=AQ=MQ

∴∠QBM=∠M=x

∴∠AQB=∠QBM+∠M=2x

由题知∠ACB=45°且AC∥DE

∴∠QDB=∠ACB=45°

∵∠QDB=∠MQD+∠M=2x

∴2x=45°即∠AQB=45°

在等腰直角△ABC中，斜边AC=2，则AB=BC=

∴BD=BC+CD=

∴四边形ABDE的面积为：

故答案为：，.

(3) 存在．

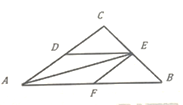
如下图，以AB为边长，在直线AB的右侧作等边三角形ABO，在以O为圆心、OA长为半径作⊙O．过点O作OM⊥MD，交⊙O于点M，点M在AC的右上方．

过点M作AC的平行线DE，AE∥BC，BC的延长线交DE于点D，AE交⊙O于点H．

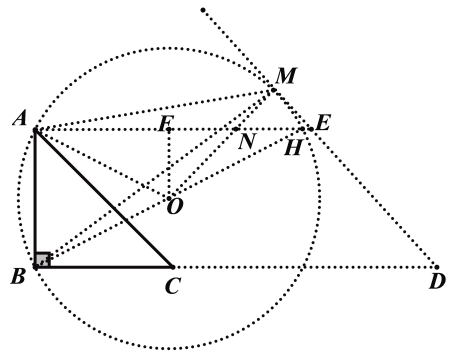
则此时满足∠AMB=30°，此时四边形ABDE的面积最大．

作OF⊥AE于F，OM与AE相交于点N．

∵AE∥CD，DE∥AC

∴四边形ACDE是平行四边形

∴AE=CD，DE=AC=2

∴∠EDC=∠ACB=45°

∴∠AEM=∠EDC=45°

∵OM⊥AC

∴OM⊥DE

∴∠NME=90°

∴NE=MN，∠MNH=45°

由（2）知，AB=BC=

∴⊙O的半径是.

连接BH，∵AE∥BC，∠ABC=90°

∴∠BAH=180°-∠ABC=90°

∵∠AMB=30°，

∴∠AHB=∠AMB=30°

∴

∵OF⊥AH，点O是圆心

∴

根据勾股定理得

∵∠FNO=∠MNH=45°

∴

∴

∴

∴

∴

故答案为：当时，四边形面积最大值为.