题目内容
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于
)的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 点,且
点,且![]() 与
与![]() 交于点
交于点![]() .
.
(1)求反比例函数的表达式及点![]() 的坐标;
的坐标;
(2)直接写出反比例函数图像位于第一象限且![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)求![]() 与
与![]() 面积的比.
面积的比.
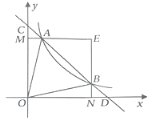
![]()
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() (3)
(3)![]() 与
与![]() 面积的比等于4:2=2:1
面积的比等于4:2=2:1
【解析】
(1)把点![]() 代入一次函数y=-x+4,即可得出a,再把点A坐标代入反比例函数,即可得出k,两个函数解析式联立求得点B坐标;
代入一次函数y=-x+4,即可得出a,再把点A坐标代入反比例函数,即可得出k,两个函数解析式联立求得点B坐标;
(2)观察图象即可写出反比例函数图像位于第一象限且![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)根据![]() 、
、![]() ,即可求得
,即可求得![]() ,
,![]() 的面积=四边形
的面积=四边形![]() 的面积-
的面积-![]() 的面积-
的面积-![]() 的面积-
的面积-![]() 的面积,即可求出它们面积的比.
的面积,即可求出它们面积的比.
(1)由已知可得,![]() ,
,![]() ,
,
![]() 反比例函数的表达式为
反比例函数的表达式为![]() ,
,
联立 ,解得
,解得![]() 或
或![]() ,
,![]() ;
;
(2)![]() 或
或![]()
(3)由![]() 、
、![]() ,可得
,可得![]()
![]() 的面积=四边形
的面积=四边形![]() 的面积-
的面积-![]() 的面积-
的面积-![]() 的面积-
的面积-![]() 的面积=3×3-2-3=4,
的面积=3×3-2-3=4,
所以![]() 与
与![]() 面积的比等于4:2=2:1
面积的比等于4:2=2:1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目