题目内容
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用60天的时间销售一种成本为10元每件的商品,经过统计得到此商品的日销售量m(件)、销售单价n(元/件)在第x天(x为正整数)销售的相关信息:
①m与x满足一次函数关系,且第1天的日销售量为98件,第4天的日销售量为92件;
②n与x的函数关系式为:n=![]() .
.
(1)求出第15天的日销售量;
(2)设销售该产品每天利润为y元,请写出y与x的函数关系式,并求出在60天内该产品的最大利润.
(3)在该产品的销售过程中,共有 天销售利润不低于2322元.(请直接写出结果)
【答案】(1)70;(2)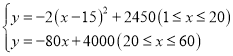 ;60天内该产品的最大利润为2450元;(3)14天
;60天内该产品的最大利润为2450元;(3)14天
【解析】
(1)利用待定系数法,求出m与x的关系式,再将x=15代入,求出m的值即可;
(2)分两种情况:当1≤x≤20时和当20≤x≤60时,分别用y=m(n﹣10)求出y与x的关系,再求出其最大值即可;
(3)分两种情况:当1≤x≤20时和当20≤x≤60时,分别求出利润不低于2322元的x的取值范围,即可得解.
解:(1)设m与x的函数关系式为:m=kx+b,
当x=1时,m=98;当x=4时,m=92,
∴![]() ,
,
解得:![]() ,
,
∴m与x的函数关系式为:m=﹣2x+100,
∴当x=15时,m=﹣2×15+100=70;
(2)根据题意,可知:
当1≤x≤20时,y=m(n﹣10)=(﹣2x+100)(x+30﹣10)=﹣2(x﹣15)2+2450,
∴当x=15时,y有最大值2450,
当20≤x≤60时,y=m(n﹣10)=40(﹣2x+100)=﹣80x+4000,
∵y随x的增大而减小,
∴当x=20时,y有最大值为:﹣1600+4000=2400,
综上所述,60天内该产品的最大利润为2450元
答: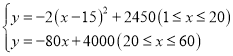 ;60天内该产品的最大利润为2450元;
;60天内该产品的最大利润为2450元;
(3)根据题意,
当1≤x≤20时,﹣2(x﹣15)2+2450≥2322,
解得:7≤x≤23,
∴7≤x≤20,其整数解为7、8、9、10、11、12、13、14、15、16、17、18、19、20
当20≤x≤60时,﹣80x+4000≥2322,
解得:x≤![]() ,
,
∴20≤x≤![]() ,其整数解为20
,其整数解为20
综上所述,销售利润不低于2322元有14天,
故答案为:14.