ƒøƒ⁄»ð
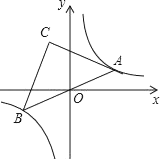
°æƒø°ø»ÁÕº£¨ƒ≥ÃÏŒ“π˙“ªÀ“∫£ºý¥¨—≤∫ΩµΩA∏€ø⁄’˝Œ˜∑ΩµƒB¥¶ ±£¨∑¢œ÷‘⁄Bµƒ±±∆´∂´60°„∑ΩœÚ£¨œýæý150∫£¿Ô¥¶µƒCµ„”–“ªø…“…¥¨÷ª’˝—ÿCA∑ΩœÚ–– ª£¨Cµ„‘⁄A∏€ø⁄µƒ±±∆´∂´30°„∑ΩœÚ…œ£¨∫£ºý¥¨œÚA∏€ø⁄∑¢≥ˆ÷∏¡Ó£¨÷¥∑®¥¨¡¢º¥¥”A∏€ø⁄—ÿAC∑ΩœÚ ª≥ˆ£¨‘⁄D¥¶≥…π¶¿πΩÿø…“…¥¨÷ª£¨¥À ±Dµ„”ÎBµ„µƒæý¿ÎŒ™![]() ∫£¿Ô£Æ
∫£¿Ô£Æ
£®1£©«ÛBµ„µΩ÷±œþCAµƒæý¿Î£ª
£®2£©÷¥∑®¥¨¥”AµΩD∫Ω––¡À∂ý…Ÿ∫£¿Ô£ø

°æ¥∞∏°ø£®1£©![]() µ„µΩ÷±œþ
µ„µΩ÷±œþ![]() µƒæý¿Î «75∫£¿Ô£ª£®2£©÷¥∑®¥¨¥”
µƒæý¿Î «75∫£¿Ô£ª£®2£©÷¥∑®¥¨¥”![]() µΩ
µΩ![]() ∫Ω––¡À
∫Ω––¡À![]() ∫£¿Ô£Æ
∫£¿Ô£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æð∑ΩŒªΩ«µƒ∂®“Âœ»«Û≥ˆ°œCBA∫Õ°œBCAµƒ∂» ˝£¨‘Ÿ∏˘æðBH=BC°¡sin°œBCAº∆À„º¥ø…µ√≥ˆ¥∞∏£ª
£®2£©—”≥§CA£¨◊˜BH°ÕCAµƒ—”≥§œþ”⁄µ„H£¨∏˘æðπ¥π…∂®¿Ì«Û≥ˆDHµƒ÷µ£¨‘Ÿ¿˚”√tan°œBAHµƒ÷µº¥ø…«Û≥ˆAHµƒ÷µ£¨º¥ø…µ√≥ˆ¥∞∏£Æ
Ω‚£∫£®1£©![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £®∫£¿Ô£©£¨
£®∫£¿Ô£©£¨
¥£∫![]() µ„µΩ÷±œþ
µ„µΩ÷±œþ![]() µƒæý¿Î «75∫£¿Ô£ª
µƒæý¿Î «75∫£¿Ô£ª
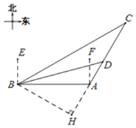
£®2£©—”≥§CA£¨◊˜BH°ÕCAµƒ—”≥§œþ”⁄µ„H
![]() ∫£¿Ô£¨
∫£¿Ô£¨![]() ∫£¿Ô£¨
∫£¿Ô£¨
![]() £®∫£¿Ô£©£¨
£®∫£¿Ô£©£¨
![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
![]() £¨
£¨
°ýAD=DH-AH=75-25![]() £®∫£¿Ô£©.
£®∫£¿Ô£©.
¥£∫÷¥∑®¥¨¥”![]() µΩ
µΩ![]() ∫Ω––¡À
∫Ω––¡À![]() ∫£¿Ô£Æ
∫£¿Ô£Æ

 ª∆∏‘–°◊¥‘™Õ¨≤Ωº∆À„ÃÏÃÏ¡∑œµ¡–¥∞∏
ª∆∏‘–°◊¥‘™Õ¨≤Ωº∆À„ÃÏÃÏ¡∑œµ¡–¥∞∏