题目内容
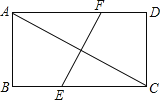
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=4,AF=6,则AC的长为( )
A.4![]() B.6
B.6![]() C.2
C.2![]() D.
D.![]()
【答案】C
【解析】
连接AE,由线段垂直平分线的性质得出OA=OC,AE=CE,证明△AOF≌△COE得出AF=CE=6,得出AE=CE=6,BC=BE+CE=10,由勾股定理求出AB的长,再由勾股定理求出AC即可.
解:如图,连接AE,设EF与AC交点为O,
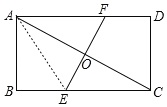
∵EF是AC的垂直平分线,
∴OA=OC,AE=CE,
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
 ,
,
∴△AOF≌△COE(ASA),
∴AF=CE=6,
∴AE=CE=6,BC=BE+CE=4+6=10,
∴AB=![]() ,
,
∴AC=![]() ,
,
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
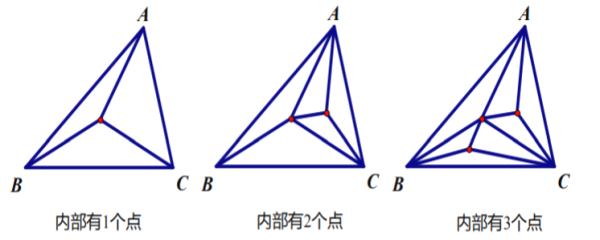
【题目】如图,![]() 内部有若干个点,用这些点以及
内部有若干个点,用这些点以及![]() 的顶点
的顶点![]() 把原三角形分割成一些三角形(互相不重叠).
把原三角形分割成一些三角形(互相不重叠).
(1)填写下表
| 1 | 2 | 3 | 4 |
分割成的三角形的个数 | 3 | 5 |
(2)如果用![]() 表示内部有
表示内部有![]() 个点时,
个点时,![]() 被分割成的三角形的个数,试写出
被分割成的三角形的个数,试写出![]() 与
与![]() 的关系式;
的关系式;
(3)原![]() 能否被分割成
能否被分割成![]() 个三角形?若能,求此时
个三角形?若能,求此时![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.