题目内容
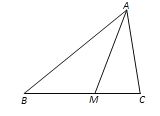
【题目】如图，在△ABC中，AC=6，∠BAC=60°，AM为△ABC的角平分线，若
，则AM长为（ ）
A.6B.
C.
D.
【答案】C
【解析】
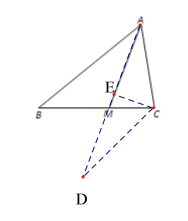
过点C作CD∥AB，交AM的延长线于点D，过点C作CE⊥AM于点E，先证CD=CA=6，利用三角函数的定义以及等腰三角形的性质，可得AD的长，再证ABM~DCM，进而即可求解．
过点C作CD∥AB，交AM的延长线于点D，过点C作CE⊥AM于点E，
∵AM为△ABC的角平分线，∠BAC=60°，
∴∠BAM=∠CAM=30°，
∵CD∥AB，
∴∠BAM=∠D，
∴∠CAM=∠D=30°，
∴CD=CA=6，
∵CE⊥AM，
∴AE=DE=ACcos30°=6×
=3
，即AD=2AE=6，
∵CD∥AB，
∴ABM~DCM，
∴
，
∴AM=
×6=
．
故选C．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
