题目内容
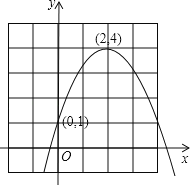
【题目】已知二次函数的图象如图所示．
（1）求这个二次函数的表达式；
（2）当﹣1≤x≤4时，求y的取值范围．
【答案】（1）y＝﹣
（x﹣2）2+4；（2）﹣
≤y≤4．
【解析】
（1）设顶点式y＝a（x﹣2）2+4，然后把（0,1）代入求出a即可得到抛物线解析式；
（2）分别计算自变量为﹣1和4对应的函数值，然后根据二次函数的性质解决问题．
解：（1）设抛物线解析式为y＝a（x﹣2）2+4，
把（0,1）代入得4a+4＝1，解得a＝﹣，
所以抛物线解析式为y＝-（x﹣2）2+4．
（2）当x＝﹣1时，y＝﹣（﹣1﹣2）2+4＝﹣；
当x＝4时，y＝﹣（4﹣2）2+4＝1，
∴ 当-1≤x≤2时，﹣≤y≤4；
当2≤x≤4时，1≤y≤4
所以当﹣1≤x≤4时，y的取值范围为﹣≤y≤4．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
