题目内容
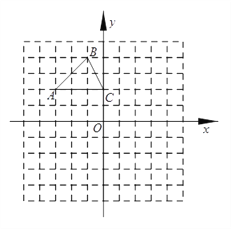
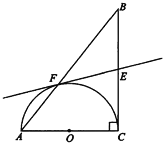
【题目】已知:如图,Rt△ABC中,∠ACB=90°,以AC为直径的半圆O交AB于F,E是BC的中点.
求证:直线EF是半圆O的切线.
【答案】证明见解析.
【解析】
连接OF,CF,由直径所对的圆周角是直角可得∠AFC=∠BFC=90°,然后由直角三角形斜边上的中线等于斜边的一半得到EF=EC,进而得到∠EFC=∠ECF,然后利用等量代换求证∠EFO=90°,得出OF⊥EF即可得证.
证明:如图,连接OF,CF,
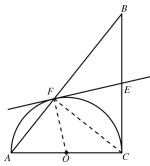
∵AC是直径,
∴∠AFC=90°,
∴∠BFC=90°,
又∵E是BC的中点,
∴EF=EC,
∴∠EFC=∠ECF,
∵OC=OF,
∴∠OFC=∠FCO,
∵∠ACB=∠FCO+∠ECF=90°,
∴∠EFC+∠OFC=90°,即∠EFO=90°,
∴OF⊥EF,
∴EF是⊙O的切线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目