题目内容
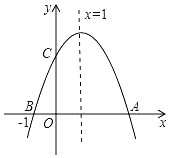
【题目】如图,一次函数y=mx+n(m≠0)的图象与反比例函数y![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(1)求该反比例函数和一次函数的表达式;
(2)根据图象直接写出当mx+n![]() 时,x的取值范围;
时,x的取值范围;
(3)直线AB交x轴于点D,过点D作直线l⊥x轴,如果直线l上存在点P,坐标平面内存在点Q,使以O、P、A、Q为顶点的四边形是矩形,直接写出点P的坐标.

【答案】(1)y![]() ,y=2x+2;(2)x>1或﹣2<x<0;(3)存在,点P的坐标为(﹣1,
,y=2x+2;(2)x>1或﹣2<x<0;(3)存在,点P的坐标为(﹣1,![]() )或(﹣1,
)或(﹣1,![]() )或(﹣1,2
)或(﹣1,2![]() )或(﹣1,2
)或(﹣1,2![]() ).
).
【解析】
(1)根据题意得出B点坐标,进而得出反比例函数解析式,再利用待定系数法得出一次函数解析式;
(2)若mx+n![]() ,结合图象可知即一次函数图象再反比例函数图象之上,结合图象即可求解;
,结合图象可知即一次函数图象再反比例函数图象之上,结合图象即可求解;
(3)若以O、P、A、Q为顶点的四边形是矩形,则存在两种情况,①若AO为边,②若AO是对角线.
(1)∵BM=OM=2,
∴点B的坐标为(﹣2,﹣2),
设反比例函数的解析式为y![]() ,
,
则﹣2![]() ,
,
得k=4,
∴反比例函数的解析式为y![]() ,
,
∵点A的纵坐标是4,
∴4![]() ,得x=1,
,得x=1,
∴点A的坐标为(1,4).
∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(﹣2,﹣2),
∴![]() ,
,
解得:![]() ,
,
即一次函数的解析式为y=2x+2;
(2)由图象可得当x>1或﹣2<x<0时,mx+n![]() ;
;
(3)存在,
若AO为边,
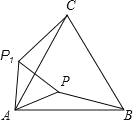
如图1,当四边形POAQ是矩形时,则∠POA=90°,
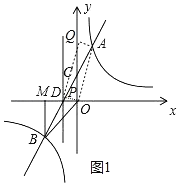
∵点A(1,4),点O(0,0),∴AO解析式为y=4x,∴直线DO解析式为:y![]() x.
x.
∵直线AB于x轴交于D,∴D(﹣1,0),∴OD=1,
设P(﹣1,a),∴a![]() ,∴点P(﹣1,
,∴点P(﹣1,![]() );
);
当四边形PAOQ是矩形,则∠PAO=90°,
同理可求:点P(﹣1,![]() );
);
若AO是对角线,
如图2,当∠APO=90°,
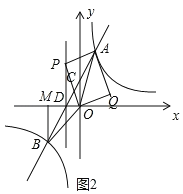
∵OP2=OA2﹣PA2=PD2+OD2,∴12+42﹣[(1+1)2+(4﹣a)2]=12+a2,
解得:a=2±![]() ,∴P(﹣1,2
,∴P(﹣1,2![]() )或(﹣1,2
)或(﹣1,2![]() ),
),
综上所述:点P的坐标为(﹣1,![]() )或(﹣1,
)或(﹣1,![]() )或(﹣1,2
)或(﹣1,2![]() )或(﹣1,2
)或(﹣1,2![]() ).
).

 名校课堂系列答案
名校课堂系列答案