题目内容
【题目】直线y=![]() x+3与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,反比例函数y=
x+3与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,反比例函数y=![]() (x<0)的图象过点C,则m=_____.
(x<0)的图象过点C,则m=_____.
【答案】﹣![]()
【解析】
过C点作CD⊥x轴于D,CE⊥y轴于E,先确定A点坐标为(-6,0),B点坐标为(0,3),再利用勾股定理计算出AB=![]() ,然后根据等腰三角形的性质得到∠ACB=90°,CA=CB=
,然后根据等腰三角形的性质得到∠ACB=90°,CA=CB=![]() AB=
AB=![]() ,由于∠DCE=90°,根据等角的余角相等得到∠ACD=∠BCE,易证得Rt△ACD≌Rt△BCE,则CD=CE,得到四边形CDOE为正方形,并且正方形CDOE的面积=四边形CAOB的面积,再计算出四边形CAOB的面积=S△CAB+S△OAB=
,由于∠DCE=90°,根据等角的余角相等得到∠ACD=∠BCE,易证得Rt△ACD≌Rt△BCE,则CD=CE,得到四边形CDOE为正方形,并且正方形CDOE的面积=四边形CAOB的面积,再计算出四边形CAOB的面积=S△CAB+S△OAB=![]() CACB+
CACB+![]() OAOB=
OAOB=![]() ,则CD=CE=
,则CD=CE=![]() ,可确定C点坐标为(-
,可确定C点坐标为(-![]() ,
,![]() ),然后把C点坐标代入反比例函数解析式即可得到m的值.
),然后把C点坐标代入反比例函数解析式即可得到m的值.
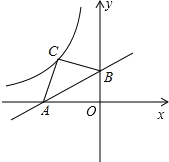
如图,过C点作CD⊥x轴于D,CE⊥y轴于E.
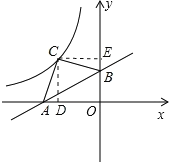
∵y=![]() x+3,∴令x=0,得y=3;令y=0,得
x+3,∴令x=0,得y=3;令y=0,得![]() x+3=0,解得:x=﹣6,∴A点坐标为(﹣6,0),B点坐标为(0,3),
x+3=0,解得:x=﹣6,∴A点坐标为(﹣6,0),B点坐标为(0,3),
在Rt△OAB中,OA=6,OB=3,∴AB=![]() =
=![]() .
.
∵△ACB为等腰直角三角形,∴∠ACB=90°,CA=CB=![]() AB=
AB=![]() ,而∠DCE=90°,∴∠ACD=∠BCE,∴Rt△ACD≌Rt△BCE,∴CD=CE,∴四边形CDOE为正方形,∴正方形CDOE的面积=四边形CAOB的面积=S△CAB+S△OAB=
,而∠DCE=90°,∴∠ACD=∠BCE,∴Rt△ACD≌Rt△BCE,∴CD=CE,∴四边形CDOE为正方形,∴正方形CDOE的面积=四边形CAOB的面积=S△CAB+S△OAB=![]() CACB+
CACB+![]() OAOB=
OAOB=![]() ×
×![]() ×
×![]() +
+![]() ×6×3=
×6×3=![]() ,∴CD=CE=
,∴CD=CE=![]() ,∴C点坐标为(﹣
,∴C点坐标为(﹣![]() ,
,![]() ),
),
把C(﹣![]() ,
,![]() )代入y=
)代入y=![]() ,得m=﹣
,得m=﹣![]() ×
×![]() =﹣
=﹣![]() .
.
故答案为:﹣![]() .
.

【题目】有这样一个问题:探究函数y![]() x的图象与性质.
x的图象与性质.
小亮根据学习函数的经验,对函数y![]() x的图象与性质进行了探究.
x的图象与性质进行了探究.
下面是小亮的探究过程,请补充完整:
(1)函数y![]() x中自变量x的取值范围是 ;
x中自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 |
|
|
|
| 3 | 4 | 5 | 6 | … |
y | … |
|
|
| 0 |
|
|
|
| m |
|
|
| … |
求m的值;
(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
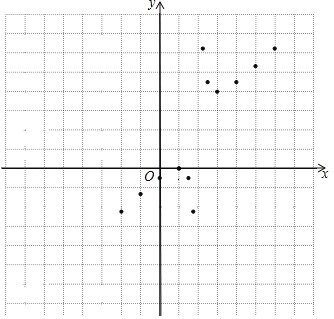
(4)根据画出的函数图象,发现下列特征:
①该函数的图象是中心对称图形,对称中心的坐标是 ;
②该函数的图象与过点(2,0)且平行于y轴的直线越来越靠近而永不相交,该函数的图象还与直线 越来越靠近而永不相交.
【题目】为拓宽学生视野,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级开展研学旅行活动,在参加此次活动的师生中,若每位老师带![]() 名学生,还剩
名学生,还剩![]() 名学生没人带;若每位老师带
名学生没人带;若每位老师带![]() 名学生,则有一位老师少带
名学生,则有一位老师少带![]() 名学生.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
名学生.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 已和客车 | |
载客量(人/量) |
|
|
租金(元/辆) |
|
|
学校计划此次研学旅行活动的租车总费用不超过![]() 元,为了安全,每辆客车上至少要有
元,为了安全,每辆客车上至少要有![]() 名老师.
名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有![]() 名老师,可求得租用客车总数为______辆.
名老师,可求得租用客车总数为______辆.
(3)在(2)的条件下,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.