题目内容
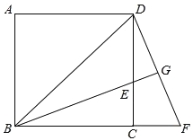
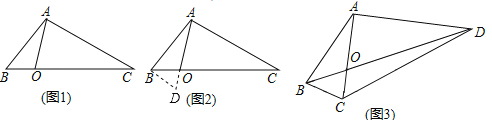
【题目】如图，已知长方形ABCD与正方形BEFM，且A、B、E在一直线上，已知AB＝a，BC＝b，BE＝c，且a＞b＞c＞0.设△ADE的面积为S1.
(1)用含a、b、c的代数式表示S1；
(2)正方形BEFM绕B顺时针旋转180度得到正方形BEFM，连接DM，用含a、b、c的代数式表示△DCM的面积为S2;
(3)请比较S1与S2的大小关系，并说明理由.
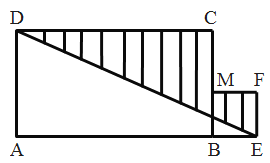
【答案】（1）S1=
；（2）S2=
，（3）S1<S2
【解析】
（1）利用三角形面积公式表示出S1即可；
（2）利用三角形面积公式表示出S1即可；
（3）求S1- S2，判断结果正负即可比较出S1和S2的大小.
（1）S1=
AD
=；
（2）如图：
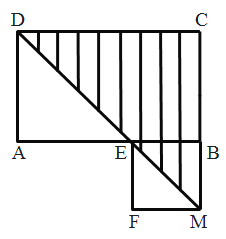
S2=CD
=，
（3）S1- S2=-=
-
=c(b-a)，
因为a＞b，
所以c(b-a)<0，
即S1<S2
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了鼓励市民节约用水，某市水费实行分段计费制，每户每月用水量在规定用量及以下的部分收费标准相同，超出规定用量的部分收费标准相同．例如：若规定用量为10吨，每月用水量不超过10吨按1.5元/吨收费，超出10吨的部分按2元/吨收费，则某户居民一个月用水8吨，则应缴水费：8×1.5=12（元）；某户居民一个月用水13吨，则应缴水费：10×1.5+（13﹣10）×2=21（元）．
表是小明家1至4月份用水量和缴纳水费情况，根据表格提供的数据，回答：
月份 | 一 | 二 | 三 | 四 |
用水量（吨） | 6 | 7 | 12 | 15 |
水费（元） | 12 | 14 | 28 | 37 |
（1）该市规定用水量为 吨，规定用量内的收费标准是 元/吨，超过部分的收费标准是 元/吨．
（2）若小明家五月份用水20吨，则应缴水费 元．
（3）若小明家六月份应缴水费46元，则六月份他们家的用水量是多少吨？
