题目内容
【题目】已知反比例函数y=![]() (m为常数)的图象经过点A(﹣1,6).
(m为常数)的图象经过点A(﹣1,6).
(1)求m的值;
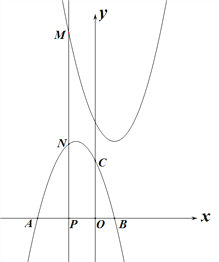
(2)如图,过点A作直线AC与函数y=![]() 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
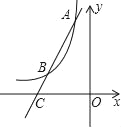
【答案】(1)m的值为2;(2)C(﹣4,0).
【解析】试题分析:(1)将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;
(2)分别过点A、B作x轴的垂线,垂足分别为点E、D,则△CBD∽△CAE,运用相似三角形知识求出CD的长即可求出点C的横坐标.
试题解析:(1)∵图象过点A(-1,6),
∴![]() ,
,
解得m=2.
(2)分别过点A、B作x轴的垂线,垂足分别为点E、D,
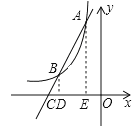
由题意得,AE=6,OE=1,即A(-1,6),
∵BD⊥x轴,AE⊥x轴,
∴AE∥BD,
∴△CBD∽△CAE,
∴![]() ,
,
∵AB=2BC,
∴![]() ,
,
∴![]() ,
,
∴BD=2.
即点B的纵坐标为2.
当y=2时,x=-3,即B(-3,2),
设直线AB解析式为:y=kx+b,
把A和B代入得:![]() ,
,
解得![]() ,
,
∴直线AB解析式为y=2x+8,令y=0,解得x=-4,
∴C(-4,0).

【题目】某商场举行“促销周”活动,每个促销日顾客人数变化如下表(正号表示人数比前一天多,负号表示比前一天少)
日期 | 第1日 | 第2日 | 第3日 | 第4日 | 第5日 | 第6日 | 第7日 |
人数变化(单位:千人) |
|
|
|
|
|
|
|
(1)本“促销周”中顾客人数最多的一天比最少的一天多几千人?
(2)若第一个促销日前一天的顾客人数为3千人,则第3个促销日的顾客人数是多少千人?
(3)如果每千人每日带来的经济收入约为5万元,则该商场本“促销周”总收入约为多少万元?
【题目】某商品根据以往销售经验,每天的售价与销售量之间有如下表的关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销售量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当单价从38元/千克下调到x元时,销售量为y千克,已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)如果某商品的成本价是20元/千克,为使某一天的利润为780元,那么这一天的销售价应为多少元?(利润=销售总金额﹣成本)