��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ ![]() �У���֪
�У���֪ ![]() ��
�� ![]() ���������ֱ�Ϊ
���������ֱ�Ϊ ![]() ��
�� ![]() ��
�� ![]() ���߶�
���߶� ![]() ��һ�㣨��
��һ�㣨�� ![]() ��
�� ![]() �㲻�غϣ���������
�㲻�غϣ��������� ![]()
![]() ��
�� ![]() ��������
�������� ![]() ��
�� ![]() ������Ϊ
������Ϊ ![]() ��������
�������� ![]()
![]() ��
�� ![]() ��������
�������� ![]() ��
�� ![]() ������Ϊ
������Ϊ ![]() ��
�� ![]() ��
�� ![]() ���ӳ����ཻ�ڵ�
���ӳ����ཻ�ڵ� ![]() ��
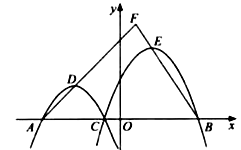
��
��1���� ![]() ��
�� ![]() ����������
���������� ![]() ��
�� ![]() �Ľ���ʽ��
�Ľ���ʽ��
��2���� ![]() ��
�� ![]() ����
���� ![]() ��ֵ��
��ֵ��
��3���Ƿ����������ʵ�� ![]() ��
�� ![]() ��������
�������� ![]() ȡ��ֵ��ֱ��
ȡ��ֵ��ֱ�� ![]() ��
�� ![]() �������ܻ��ഹֱ�������ڣ���ֱ��д��
�������ܻ��ഹֱ�������ڣ���ֱ��д�� ![]() ��������ͬ��ֵ���������ڣ���˵�����ɣ�
��������ͬ��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����ɵã�
��� ��
����������L1�Ľ���ʽΪy=-![]() x2-
x2-![]() x-2.
x-2.
ͬ����
��� ��
����������L2�Ľ���ʽΪy= -![]() x2+
x2+![]() x+2.
x+2.
��2��
�⣺��ͼ������D��DG��x���ڵ�G������E��EH��x���ڵ�H.
����ɵã�![]()
���![]()
��������L1�Ľ���ʽΪy=-x2+��m-4��x+4m.
���D��������-![]() ,
,![]() ��.
��.
��DG=![]() =
=![]() ,AG=
,AG=![]() .
.
ͬ���ɵã�������L2�Ľ���ʽΪy=-x2+��m+4��x-4m
EH=![]() =
=![]() ��BH=
��BH=![]() .
.
��AF��BF��DG��x�ᣬEH��x��
���AFB=��AGD=��EHB=90��
���ADG=��ABF=90��-��BAF
���ADG�ס�EBH
��![]() =
=![]() .
.
�� =
=![]()
��m=2![]() ��m=-2
��m=-2![]() .
.

��3��
�⣺���ڣ�����a=-![]() ,a=-
,a=-![]() .
.
����������1����a��m����õ���֪�㣬�ѵ���뺯������ʽ���ɷ����飬���ݴ���ϵ�����������������ʽ.
��2����ͼ������D��DG��x���ڵ�G������E��EH��x���ڵ�H����a=-1���뺯������ʽ��Ȼ���ϣ�m,0���ͣ�-4��0������ɽ����������ʽL1 �� Ȼ��ֱ����D�����꣬�õ�DG,AG�ij���ͬ���õ�L2;���EH,BH�ij����ٸ������������Ƶ��ж������ʹ��췽����⼴��.
��3������ǰ��Ľ��ֱ��д������.
�����㾫����������Ҫ���������������ε��ж������ʵ����֪ʶ�㣬��Ҫ�������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��������ȷ�����⣮

 ��У����ϵ�д�
��У����ϵ�д�