题目内容
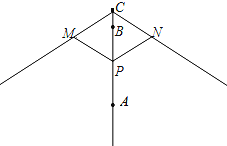
【题目】如图，已知△ABC中，∠B=∠C，AB=8厘米，BC=6厘米，点D为AB的中点．如果点P在线段BC上以每秒2厘米的速度由B点向C点运动，同时，点Q在线段CA上以每秒a厘米的速度由C点向A点运动，设运动时间为t（秒）（0≤t≤3）．
（1）用的代数式表示PC的长度；
（2）若点P、Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
（3）若点P、Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等？
【答案】（1）PC= 6﹣2t；
（2）△BPD和△CQP全等，理由见解析；
（3）VQ
厘米/秒．
【解析】
试题分析：（1）先表示出BP，根据PC=BC﹣BP，可得出答案；
（2）根据时间和速度分别求得两个三角形中的边的长，根据SAS判定两个三角形全等．
（3）根据全等三角形应满足的条件探求边之间的关系，再根据路程=速度×时间公式，先求得点P运动的时间，再求得点Q的运动速度；
解：（1）BP=2t，则PC=BC﹣BP=6﹣2t；
（2））△BPD和△CQP全等
理由：∵t=1秒∴BP=CQ=2×1=2厘米，
∴CP=BC﹣BP=6﹣2=4厘米，
∵AB=8厘米，点D为AB的中点，
∴BD=4厘米．
∴PC=BD，
在△BPD和△CQP中，
，
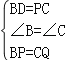∴△BPD≌△CQP（SAS）；
（3）∵点P、Q的运动速度不相等，
∴BP≠CQ
又∵△BPD≌△CPQ，∠B=∠C，
∴BP=PC=3cm，CQ=BD=4cm，
∴点P，点Q运动的时间t=
=
秒，
∴VQ=
=
=厘米/秒．
【题目】学习完一次函数后，小荣遇到过这样的一个新颖的函数：y=|x﹣1|，小荣根据学校函数的经验，对函数y=|x﹣1|的图象与性质进行了探究．下面是小荣的探究过程，请补充完成：
（1）列表：下表是y与x的几组对应值，请补充完整．
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 4 | 2 | 1 | … |
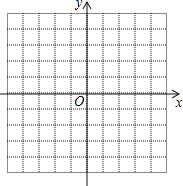
（2）描点连线：在平面直角坐标系xOy中，请描出以上表中各对对应值为坐标的点，画出该函数的图象；
（3）进一步探究发现，该函数图象的最低点的坐标是（1，0），结合函数的图象，写出该函数的其他性质（一条即可）： ．
