题目内容
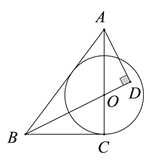
【题目】如图,已知在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() 与
与![]() 的平分线,
的平分线,![]() 的延长线与
的延长线与![]() 相交于点
相交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
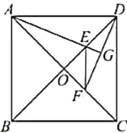
A.①②B.③④C.①②③D.①②③④
【答案】C
【解析】
由正方形的性质可得∠ACD=∠ADB=45°,根据三角形外角性质及角平分线的定义可得∠AFD=∠ADF,可证明AF=AD,根据等腰三角形“三线合一”的性质可得AG⊥DF,可得AG为DF的垂直平分线,可判定①正确;根据垂直平分线的性质可得EF=ED,可得∠EFD=∠EDF,即可证明∠EFD=∠FDC,可得EF//CD,即可证明EF//AB,可判定②正确;根据正方形的性质可得AB=AD,即可证明AB=AF,可判定③正确,由EF=ED,EF为Rt△EOF的斜边,可得ED>OE,即可得出EF不是△OCD的中位线,可得CD≠2EF,根据AB=CD即可判定④错误;综上即可得答案.
∵在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,
∴∠ACD=∠ADB=45°,∠DOC=90°,AB=AD,
∵DF为∠ODC的平分线,
∴∠ODF=∠CDF,
∴∠ADB+∠ODF=∠ACD+∠CDF,即∠AFD=∠ADF,
∴AD=AF,
∵AG为∠OAD的平分线,
∴AG⊥DF,故①正确,
∴AG为DF的垂直平分线,
∴ED=EF,
∴∠EFD=∠EDF,
∴∠EFD=∠CDF,
∴EF//CD,
∵AB//CD,
∴EF//AB,故②正确,
∵AD=AB,AD=AF,
∴AB=AF,故③正确,
∵EF=ED,EF为Rt△EOF的斜边,
∴ED>OE,
∵EF//CD,
∴EF不是△OCD的中位线,
∴CD≠2EF,即AB≠2EF,故④错误,
综上所述:正确的结论有①②③,
故选:C.

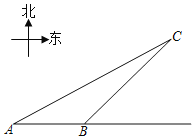
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
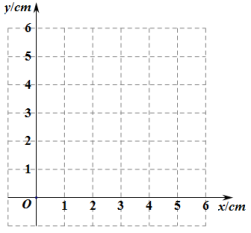
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.