题目内容
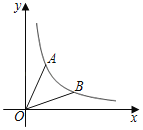
【题目】如图,已知点A(t,1)在第一象限,将OA绕点O顺时针旋转45°得到OB,若反比例数y=![]() (k>0)的图象经过点A、B,则k=_____.
(k>0)的图象经过点A、B,则k=_____.
【答案】![]() ﹣1.
﹣1.
【解析】
根据反比例函数图象关于直线y=x的对称性得,B(1,t),过点A作AC⊥y轴于点C,BE⊥x轴于点E,又由k的几何意义可得k=t,作AO的垂直平分线DE,可得∠CDA=45°,连接AD,根据OC=OD+DC,即1=![]() t+t,进而求出t的值,即为k的值.
t+t,进而求出t的值,即为k的值.
解:如图,点A(t,1),将OA绕点O顺时针旋转45°得到OB,
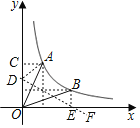
根据反比例函数图象关于直线y=x的对称性得,
B(1,t),
过点A作AC⊥y轴于点C,BE⊥x轴于点E,
又由k的几何意义可知:
k=1×t=t,
∵∠AOB=45°,
∴∠AOC=∠BOE=22.5°,
∴tan∠AOC=tan22.5°=![]() =t=k,
=t=k,
作AO的垂直平分线DF,连接AD,
∴AD=OD,
∴∠DAO=∠DOA=22.5°,
∴∠CDA=45°,
∴DC=CA=t,
∴AD=DO=![]() t,
t,
∴OC=OD+DC,
即1=![]() t+t,
t+t,
解得t=![]() ﹣1.
﹣1.
所以k=![]() ﹣1.
﹣1.
故答案为:![]() ﹣1.
﹣1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目