题目内容
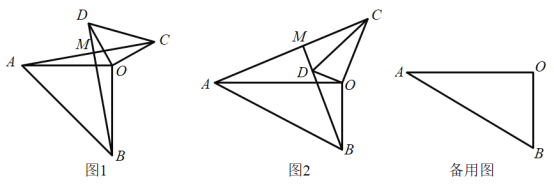
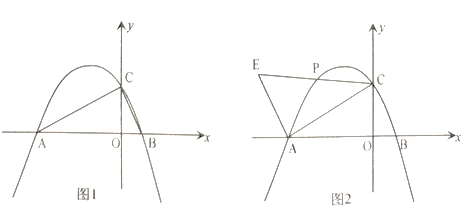
【题目】如图1,已知开口向下的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 不小于
不小于![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求系数![]() 的取值范围;
的取值范围;
请你根据自身能力从![]() 或(4)小题中任选-题作答.
或(4)小题中任选-题作答.
(3)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 试探究是否存在点
试探究是否存在点![]() ,使得
,使得![]() 的某一个角等于
的某一个角等于![]() 的
的![]() 倍?若存在,求点
倍?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
(4)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 抛物线的对称轴与
抛物线的对称轴与![]() 轴交于点
轴交于点![]() 连接
连接![]() 试探究是否存在点
试探究是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,求点
相似?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在符合条件的两点
;(3)存在符合条件的两点![]() ,其横坐标为
,其横坐标为![]() 或
或![]() ;(4)存在符合条件的两点
;(4)存在符合条件的两点![]() 其横坐标为
其横坐标为![]() 或
或![]() .
.
【解析】
(1)令y=0,求解即可得到A、B的坐标;令x=0,即可求得C点坐标,进而得到答案;
(2)先证明 ![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,求出OC的长度,再根据
,求出OC的长度,再根据![]() 不小于90°得到
不小于90°得到![]() 即可求出a的范围;
即可求出a的范围;
(3)在![]() 上取点
上取点![]() 使
使![]() 得到
得到![]() 根据勾股定理求出
根据勾股定理求出![]() 的长, 根据
的长, 根据![]() 得到
得到![]() .再分情况讨论即可得到答案;
.再分情况讨论即可得到答案;
(4)分情况讨论当![]() 得到
得到![]() 再过点
再过点![]() 作
作![]() 轴于点
轴于点![]() 求出点
求出点![]() 的坐标,进而得到P的横坐标,再讨论当
的坐标,进而得到P的横坐标,再讨论当![]() ,类似求解即可得到答案;
,类似求解即可得到答案;
![]() 令
令![]() 得
得![]()
解得![]() ,
,
令![]() 得
得![]() ,
,
![]()
![]() 当
当![]() 时,
时,
![]()
![]()
![]()
![]()
![]()
![]() 不小于
不小于![]()
![]()
![]() ,
,
![]()
又![]()
![]()
![]() 存在.当
存在.当![]() 时,
时,
![]()
![]()
![]() ,
,![]()
在![]() 上取点
上取点![]() 如下图,使
如下图,使![]()
则![]()
设![]() 的长为
的长为![]() ,则
,则![]()
在![]() 中,
中,![]()
![]()
![]()
![]() .
.
①当![]() 时,
时,![]()
![]()
![]()
![]()
过点![]() 作
作![]() 轴于点
轴于点![]()
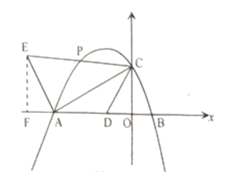
![]() ,
,
![]()
![]()
![]()
![]()
又![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 抛物线解析式为
抛物线解析式为![]()
![]()
![]() (舍去),
(舍去),![]()
②当![]() 时,
时,![]()
![]()
![]()
![]() 时,
时,
同上可得![]() ,直线
,直线![]() 的解析式为
的解析式为![]()
![]()
![]() (舍去),
(舍去),![]() .
.
综上所述,存在符合条件的两点![]()
其横坐标为![]() 或
或![]()
![]() 存在.当
存在.当![]() 时,
时,
![]()
![]()
当![]()
即![]() 时,
时,![]()
过点![]() 作
作![]() 轴于点
轴于点![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
又![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 抛物线解析式为
抛物线解析式为![]()
![]()
![]() (舍去),
(舍去),![]()
当![]() ,
,
即![]() 时,
时,![]()
同上可得![]() ,
,
直线![]() 的解析式为
的解析式为![]()
![]()
![]() (舍去),
(舍去),![]()
综上所述,存在符合条件的两点![]() 其横坐标为
其横坐标为![]() 或
或![]() .
.

【题目】某初中学校每个年级学生刚好为500人,为了解数学史知识的普及情况,随机从每个年级各抽10名学生进行测试,测试成绩整理如下:
年级 | 学生测试成绩表 | |||||||||
七年级 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
八年级 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
九年级 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求每个年级恰好都有一名学生参加的概率.
【题目】张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
①2019年10月至2020年3月通话时长统计表
时间 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
时长(单位:分钟) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月与2020年5月,这两个月通话时长的总和为1100分钟根据以上信息,推断张老师这八个月的通话时长的中位数可能的最大值为( )
A.550B.580C.610D.630