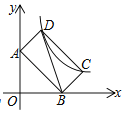
题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的正半轴交于点A,抛物线的顶点为B,直线
轴的正半轴交于点A,抛物线的顶点为B,直线![]() 经过A,B两点,且
经过A,B两点,且![]() .
.
(1)求抛物线的解析式
(2)点P在第一象限内对称轴右侧的抛物线上,其横坐标为![]() ,连接OP,交对称轴于点C,过点C作
,连接OP,交对称轴于点C,过点C作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,连接
,连接![]() ,设线段
,设线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,交
,交![]() 于点F,点G是BE的中点,过点G作
于点F,点G是BE的中点,过点G作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,当
,当![]() 且
且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
【答案】(1)抛物线解析式为![]() ;(2)
;(2)![]() ,自变量的取值范围是
,自变量的取值范围是![]() ;(3)
;(3)![]() ,点
,点![]() 的坐标为
的坐标为![]()
【解析】
(1)过点B作BC⊥OA垂足为C.令y=0可求得点A的坐标,由抛物线的对称性可得到AC=3,然后依据锐角三角形函数的定义可得到BC的长,从而得到点B的坐标;将点A和点B的坐标代入抛物线的解析式,可求得a、b的值,于是可求得抛物线的解析式;
(2)先求得直线AB的解析式,设P的坐标为(t,-t2+6t),可求得直线OP的解析式为y=(-t+6)x,接下来,求得点C的纵坐标,从而得到D点的纵坐标为-3t+18.接下来将点D点的纵坐标代入直线AB的解析式可求得点D的横坐标,然后根据P点和D点的横坐标相同,可至PD的长等于P、D两点的纵坐标之差;
(3)延长PQ交y轴于点H,过点P作PM∥x轴.先证明∠PMH=∠PMO,于是可证明△PHM≌△POM,由全等三角形的性质可得到HM=OM,设P(a,-a2+6a),则H(0,-2a2+12a).接下来,求得PH的解析式(用含a的式子表示);于是可求得点E的纵坐标为,由中点坐标公式可求得F的坐标(用含a的式子表示),将F的坐标代入直线AB的解析式可求得a的值,于是可求得点P的坐标、PH的解析式、点E的坐标,然后依据中点坐标公式可求得点G的坐标,从而得到点Q的纵坐标,然后将点Q的纵坐标代入PH的解析式可求得点Q的横坐标,于是可求得点Q的坐标,最后将点Q的坐标代入抛物线的解析式即可作出判断.
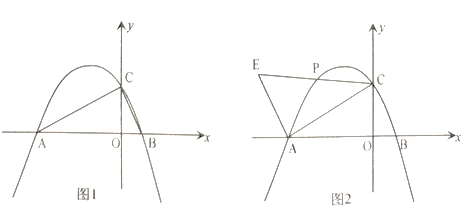
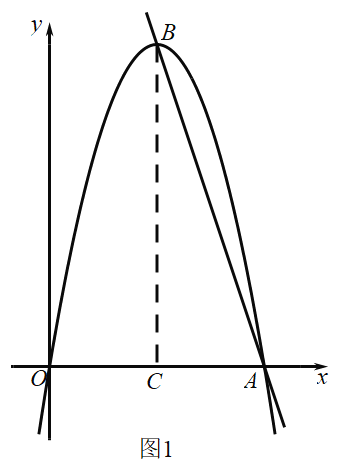
(1)如图1所示,过点B作![]() ,
,
令![]() 则
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
因为抛物线经过点![]() ,且B为顶点,
,且B为顶点,
所以![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() ,
,
所以抛物线解析式为![]() .
.
(2)如图2所示,
设直线AB解析式为![]() ,
,
则![]() ,
,
解得![]() ,
,
所以直线解析式为![]() ,
,
设点P的坐标为![]() ,OP的解析式为
,OP的解析式为![]() ,
,
![]() ,
,
将![]() 代入解析式得
代入解析式得![]() ,
,
![]() ,
,
![]() 轴,
轴,![]() 的纵坐标为
的纵坐标为![]() ,
,
将![]() 代入直线AB的解析式得:
代入直线AB的解析式得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,![]() ,
,
自变量的取值范围是![]() .
.
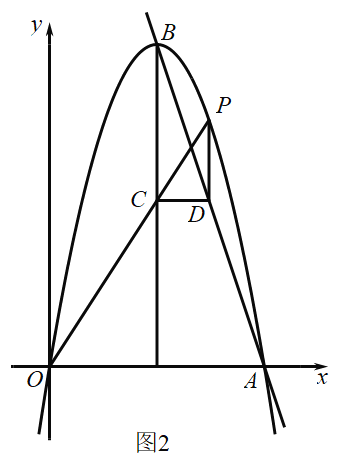
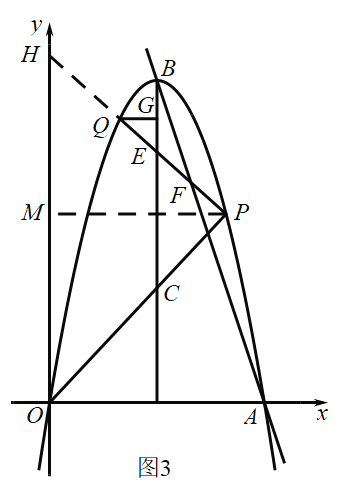
如图3所示:延长![]() 交
交![]() 轴于
轴于![]() 点,过点P作
点,过点P作![]() 轴,
轴,
![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() ,
,
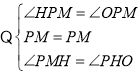 ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
设PH的解析式为![]() ,
,
将点P的坐标代入得:![]() ,
,
解得![]() ,
,
所以直线PH的解析式为![]() ,
,
将![]() 代入得解析式为
代入得解析式为![]() ,
,
所以点E的纵坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
将![]() 代入AB的解析式得:
代入AB的解析式得:![]() ,
,
![]() ,
,
整理得:![]() ,
,
解得![]() 或
或![]() (舍去)
(舍去)
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
所以直线PH的解析式为![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,所以
轴,所以![]() 的纵坐标为8,
的纵坐标为8,
将![]() 代入
代入![]() ,得
,得![]() ,
,
解得![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.

【题目】张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
①2019年10月至2020年3月通话时长统计表
时间 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
时长(单位:分钟) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月与2020年5月,这两个月通话时长的总和为1100分钟根据以上信息,推断张老师这八个月的通话时长的中位数可能的最大值为( )
A.550B.580C.610D.630