题目内容
【题目】在![]() 和
和![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.
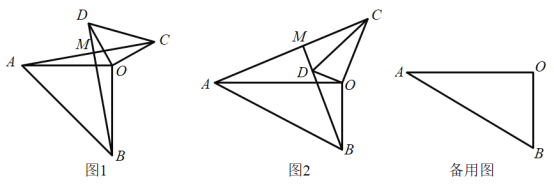
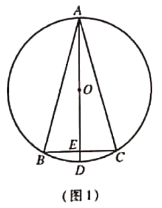
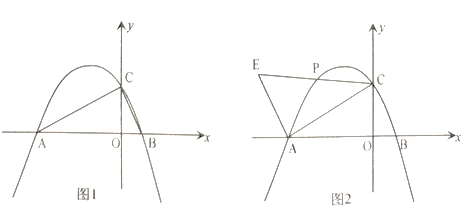
(1)如图1,若![]() ,填空:①
,填空:①![]() 的值为____________;
的值为____________;
②![]() 的度数为___________.
的度数为___________.
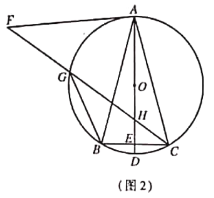
(2)如图2,若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示)及
的式子表示)及![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,
,![]() ,将三角形
,将三角形![]() 绕着点
绕着点![]() 在平面内旋转,直接写出当点
在平面内旋转,直接写出当点![]() 、
、![]() 、
、![]() 在同一直线上时,线段
在同一直线上时,线段![]() 的长.
的长.
【答案】(1)①1;②![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)①先根据等腰三角形的判定与性质可得![]() ,再根据三角形全等的判定定理与性质即可得;
,再根据三角形全等的判定定理与性质即可得;
②先根据①三角形全等的性质可得![]() ,再根据直角三角形的性质、等量代换即可得;
,再根据直角三角形的性质、等量代换即可得;
(2)先利用正切函数值可得![]() ,再利用相似三角形的判定与性质即可得
,再利用相似三角形的判定与性质即可得![]() ;先根据相似三角形的性质可得
;先根据相似三角形的性质可得![]() ,再根据直角三角形的性质、等量代换即可得;
,再根据直角三角形的性质、等量代换即可得;
(3)先利用直角三角形的性质可得AB、CD的长,再同(2)可得![]() ,
,![]() ,然后分如图3-1和如图3-2(见解析)两种情况,在
,然后分如图3-1和如图3-2(见解析)两种情况,在![]() 中,分别利用勾股定理即可得.
中,分别利用勾股定理即可得.
(1)①![]() ,
,![]()
![]()
![]() 和
和![]() 均为等腰直角三角形
均为等腰直角三角形
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,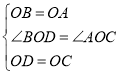
![]()
![]()
即![]()
故答案为:1;
②由①已证:![]()
![]()
![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
![]()
故答案为:![]() ;
;
(2)在![]() 中,
中,![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,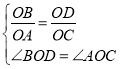
∴![]()
∴![]() ,
,![]()
![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ;
;
(3)在![]() 中,
中,![]() ,
,![]()
![]()
在![]() 中,
中,![]() ,
,![]()
![]()
同(2)可得:![]() ,
,![]()
设![]() ,则
,则![]()
由题意,分以下两种情况:
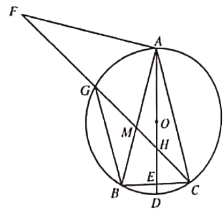
①如图3-1,点D在线段AC上
则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]()
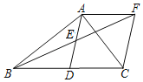
②如图3-2,点C在线段AD上
则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]()
综上,线段![]() 的长为
的长为![]() 或
或![]() .
.


练习册系列答案
相关题目