题目内容
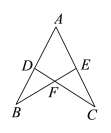
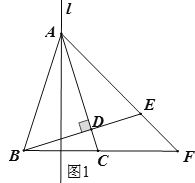
【题目】如图，点A在直线l上，点B在直线l外，点B关于直线l的对称点为C，连接AC，过点B作BD⊥AC于点D，延长BD至E使BE=AB，连接AE并延长与BC的延长线交于点F.
（1）补全图形；
（2）若∠BAC=2α，求出∠AEB的大小（用含α的式子表示）；
（3）用等式表示线段EF与BC的数量关系，并证明.
【答案】（1）见解析；（2）∠AEB=
；（3）BC=
，证明见解析.
【解析】
（1）根据题意作图即可补全图形；
（2）先根据直角三角形两锐角互余的性质求出∠ABD，再由BE=AB，可得∠AEB=∠BAE，然后利用三角形的内角和定理即可求得结果；
（3）设l与BC交于点H，过点E作EG⊥BF于点G，如图3，先利用轴对称的性推出∠BAH=∠CAH=α，再根据质余角的性质推出∠CBD=∠CAH=α，进一步利用（2）的结论和三角形的外角性质推出∠F=45°，进而可得
，然后根据AAS可证明△ABH≌△BEG，从而得BH=EG，而BC=2BH，进一步即可得出EF与BC的数量关系.
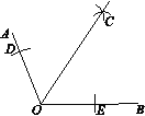
解：（1）补全图形如图1所示：
（2）∵BD⊥AC，∠BAD=2α，∴∠ABD=90°－2α，
∵BE=AB，∴∠AEB=∠BAE=
；
（3）线段EF与BC的数量关系是：BC=.
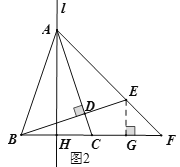
证明：设l与BC交于点H，过点E作EG⊥BF于点G，如图2，
∵点B关于直线l的对称点为C，∠BAC=2α，
∴BH=CH，∠BAH=∠CAH=α，
∵AH⊥BC，BD⊥AC，∴∠CAH+∠ACH=90°，∠CBD+∠ACH=90°，
∴∠CBD=∠CAH=α，
∵∠AEB
，∠AEB=∠CBD+∠F，
∴∠F=45°，则△EFG为等腰直角三角形，∴，
∵∠BAH=∠EBG=α，∠AHB=∠BGE=90°，AB=BE，
∴△ABH≌△BEG（AAS），
∴BH=EG，
∵BC=2BH，∴BC=2EG=.
