题目内容
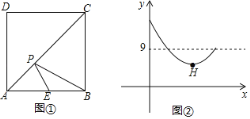
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于E.
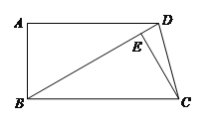
(1)求证:BE=AD;(2)若∠DCE=15°,AB=2,求在四边形ABCD的面积.
【答案】(1)见解析;(2)S四边形ABCD=![]() .
.
【解析】
(1)直接证明△ABD≌△ECB即可;
(2)由∠DCE=15°求出∠ADB=30°,然后根据含30°的直角三角形的性质得到BD=4,AD=![]() ,CE=AB=2,最后计算
,CE=AB=2,最后计算![]()
![]() +
+![]() 即可.
即可.
解:(1)证明:∵∠A=90°,CE⊥BD于E,
∴![]() .
.
∵AD∥BC,
∴![]() .
.
又∵BD=BC,
∴△ABD≌△ECB.
∴BE=AD.
(2)∵∠DCE=15°,CE⊥BD于E,
∴∠BDC=∠BCD=75°,
∴∠BCE=60°,∠CBE=∠ADB=30°,
在Rt△ABD中,∠ADB=30°,AB=2.
∴BD=4,AD=![]() .
.
∴![]()
![]() .
.
∵△ABD≌△ECB.
∴CE=AB=2.
∴![]()
![]() .
.
∴![]()
![]() +
+![]()
![]()

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目