题目内容
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )

A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
【答案】C
【解析】试题解析:∵正方形OABC的边长是6,
∴点M的横坐标和点N的纵坐标为6,
∴M(6, ![]() ),N(
),N(![]() ,6),
,6),
∴BN=6-![]() ,BM=6-
,BM=6-![]() ,
,
∵△OMN的面积为10,
∴6×6-![]() ×6×
×6×![]() -
-![]() ×6×
×6×![]() -
-![]() ×(6-
×(6-![]() )2=10,
)2=10,
∴k=24,
∴M(6,4),N(4,6),
作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,
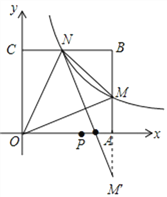
∵AM=AM′=4,
∴BM′=10,BN=2,
∴NM′=![]() =
=![]() =2
=2![]() .
.
故选C.

练习册系列答案
相关题目