题目内容
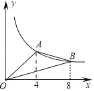
【题目】如图,直线AB与x轴,y轴分别交于点A(2,0),点B(0,2![]() ),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以
),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以![]() 个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F
个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F
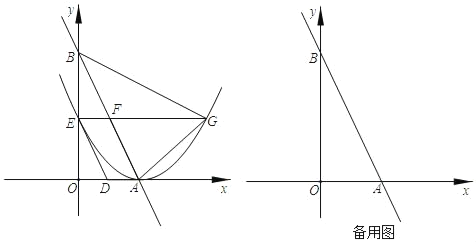
(1)求∠OAB度数;
(2)当t为何值时,四边形ADEF为菱形,请求出此时二次函数解析式;
(3)是否存在实数t,使△AGF为直角三角形?若存在,求t的值;若不存在,请说明理由.
【答案】(1)∠OAB=60°;(2)t=![]() 或t=4,四边形ADEF为菱形,
或t=4,四边形ADEF为菱形,![]() ;(3)存在,t=
;(3)存在,t=![]() ,使△AGF为直角三角形,见解析.
,使△AGF为直角三角形,见解析.
【解析】
(1)在Rt△BOA中,OA=2,OB=2![]() ,根据锐角三角函数的定义即可得出tan∠OAB的值,进而得出∠OAB的度数;
,根据锐角三角函数的定义即可得出tan∠OAB的值,进而得出∠OAB的度数;
(2)证明DE∥AB,可得四边形ADEF为平行四边形,当AD=DE时,四边形ADEF为菱形,用t表示出AD,DE的长,解方程即可得出t的值,再设顶点式可求得此时二次函数的解析式;
(3)由题意可得∠GFA=∠BAO=60°,∠FGA≠90°,所以使△AGF为直角三角形,只能是∠FAG=90°,用t分别表示出AF,FG的长,根据FG=2AF,即可得出t的值.
解:(1)∵直线AB与x轴,y轴分别交于点A(2,0),点B(0,2![]() ),∠BOA=90°,
),∠BOA=90°,
∴OA=2,OB=2![]() ,
,
∴tan∠OAB=![]() ,
,
∴∠OAB=60°;
(2)∵AD=t,BE=![]() tm
tm
∴![]() ,
,
∴DE∥AB,
∴∠EDO=∠BAO=60°,
∵过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F,
∴四边形ADEF为平行四边形,
当AD=DE时,四边形ADEF为菱形,
∵OD=2﹣t或OD=t﹣2,DE=2OD,
∴DE=4﹣2t或DE=2t﹣4,
∴t=4﹣2t或t=2t﹣4,
解得:t=![]() 或t=4,
或t=4,
当t=![]() 时,点E坐标为(0,
时,点E坐标为(0,![]() ),
),
设二次函数解析式为y=a(x﹣2)2,
将点E坐标代入,可得a=![]() ,
,
∴二次函数解析式为y=![]() (x﹣2)2;
(x﹣2)2;
当t=4时,点E坐标为(0,![]() ),
),
设二次函数解析式为y=a(x﹣2)2,
将点E坐标代入,可得a=![]() ,
,
∴二次函数解析式为y=![]() (x﹣2)2;
(x﹣2)2;
(3)∵EG∥OA,
∴∠GFA=∠BAO=60°,
∵G在二次函数图象上,
∴∠FGA≠90°,
∴使△AGF为直角三角形,只能是∠FAG=90°,
由对称性可得,EG=4,
∵四边形ADEF为平行四边形,
∴EF=AD=t,AF=DE=2(2﹣t),
∵FG=2AF,
∴4﹣t=4(2﹣t),
解得:t=![]() ,
,
∴存在实数t=![]() ,使△AGF为直角三角形.
,使△AGF为直角三角形.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案