题目内容
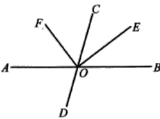
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,.
,.
(1)图中∠BOE的补角是
(2)若∠COF=2∠COE,求![]() 的度数;
的度数;
(3) 试判断OF是否平分∠AOC,并说明理由;请说明理由.
【答案】(1)∠AOE和∠DOE;(2)30°;(3)OF平分∠AOC,理由见解析.
【解析】
(1)根据补角的定义可以得出结果,另外注意∠BOE=∠COE,不要漏解;
(2)根据∠COE与∠COF互余,以及∠COF=2∠COE,可以求出∠COE的度数,又OE为∠BOC的平分线可以得出结果;
(3)根据邻补角的性质、角平分线的定义解答.
解:(1)∵OE平分∠BOC,∴∠BOE=∠COE,
∵∠COE+∠DOE=180°,
∴∠BOE+∠DOE=180°.
又∵∠AOE+∠BOE=180°,
所以∠BOE的补角为∠AOE和∠DOE;
(2)∵![]() ,
,
∴∠COE+∠COF=90°,
又∠COF=2∠COE,
∴∠COE=30°.
∴∠BOE=∠COE=30°;
(3)∵OE⊥OF,
∴∠EOF=90°,
∴∠COF=90°-∠COE.
又∵∠AOF=180°-∠EOF-∠BOE=90°-∠BOE,
又∠BOE=∠COE,
∴∠COF=∠AOF,
∴OF平分∠AOC.

练习册系列答案
相关题目