题目内容
【题目】已知抛物线y=ax2+bx+c经过原点O及点A（﹣4，0）和点C（2，3）．
（1）求抛物线的解析式及顶点坐标；
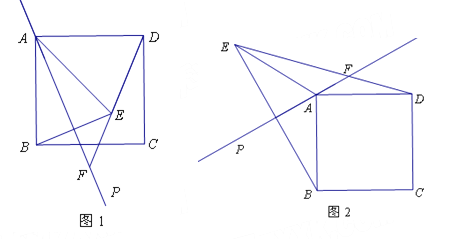
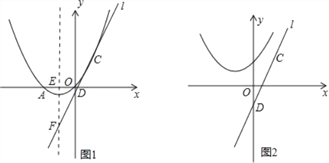
（2）如图1，设抛物线的对称轴与x轴交于点E，将直线y=2x沿y轴向下平移n个单位后得到直线l，若直线l经过C点，与y轴交于点D，且与抛物线的对称轴交于点F．若P是抛物线上一点，且PC=PF，求点P的坐标；
（3）如图2，将（1）中所求抛物线向上平移4个单位得到新抛物线，求新抛物线上到直线CD距离最短的点的坐标．（直接写出结果，不要解答过程）
【答案】(1) y=
x2+x, 顶点坐标为（﹣2，﹣1）；(2) （﹣3+
，
）或（﹣3﹣，
）；
(3) （2，7）．
【解析】分析：（1）根据待定系数法，可得函数解析式，根据配方法，可得顶点极坐标；
（2）根据待定系数法，可得直线l的解析式，根据中点坐标公式，可得D是CF的中点，根据勾股定理，可得EF，EC，根据线段垂直平分线的性质，可得ED是线段CF直平分线，根据解方程组，可得P点坐标；
（3）根据平移，可得新抛物线，根据平行于直线与抛物线相切的点到直线的距离最短，可得切线，根据解方程组，可得答案．
详解：（1）∵抛物线y=ax2+bx+c经过原点O及点A（-4，0）和点C（2，3），
∴
，解得
，
∴抛物线的解析式为y=x2+x；
∵y=x2+x=（x+2）2-1，
∴抛物线的顶点坐标为（-2，-1）；
（2）如图1：
直线l的解析式为y=2x-n，
∵直线l过点C（2，3），
∴n=1，
∴直线l的解析式为y=2x-1，当x=0时，y=-1，即D（0，-1）．
∵抛物线的对称轴为x=-2，
∴E（-2，0）．
当x=-2时，y=2x-1=-5，即F（-2，-5），
∴CD=DF=2，
∴点D是线段CF的中点，
∵C（2，3），
∴EF=EC=5，
∴ED垂直平分CF．
∴PC=PF，
∴点P在CF的垂直平分线上，
∴点P是抛物线与直线ED的交点．
ED的解析式为y=-
x-1．
联立抛物线与ED，得
，
解得
，
，
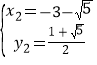点P的坐标（-3+，）或（-3-，）；
（3）如图2：
移后的抛物线为y=x2+x+4
平行于CD与物线相切的直线为y=2x+b，
联立，得x2+x+4=2x+b
方程有相等二实根，得
△=b2-4ac=（-1）2-4×（4-b）=0
解得b=3．
x2-x+1=0，
解得x=2，y=2x+3=7，
新抛物线上到直线CD距离最短的点的坐标是（2，7）．
